题目内容
8.已知△ABC的内角A,B,C所对的边分别为a,b,c.若B=2A,a=1,b=$\frac{\sqrt{6}+\sqrt{2}}{2}$,则c=1.分析 利用三角函数的倍角公式以及正弦定理和余弦定理,建立方程关系进行求解即可.
解答 解:∵B=2A,a=1,b=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∴由正弦定理得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{b}{2sinAcosA}$,
即cosA=$\frac{b}{2a}$=$\frac{\frac{\sqrt{6}+\sqrt{2}}{2}}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
又cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
c2=b2+a2-2abcosA=($\frac{\sqrt{6}+\sqrt{2}}{2}$)2+1-2×1×$\frac{\sqrt{6}+\sqrt{2}}{2}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$=1,
即c=1,
故答案为:1.
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理建立方程关系是解决本题的关键.

练习册系列答案
相关题目
18.已知A、B为△ABC的内角,向量$\overrightarrow{m}$=(sinA,sinB),$\overrightarrow{n}$=(cosB,cosA),$\overrightarrow{m}$$•\overrightarrow{n}$=$\frac{5}{13}$,tanA=$\frac{4}{3}$,则cosB的值为( )
| A. | -$\frac{16}{65}$ | B. | $\frac{16}{65}$ | C. | $\frac{63}{65}$ | D. | -$\frac{63}{65}$ |
19.若sinα=$-\frac{1}{2}$,α∈(-$\frac{π}{2}$,0),则tanα等于( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
16.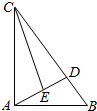 如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
 如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )
如图所示,在Rt△ABC中,∠BAC=90°,AB=2,BC=4,BD=$\frac{1}{4}$BC,E是AD的中点,则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是( )| A. | 3 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3}{2}$ |
3.抛物线的顶点在原点,焦点在x轴上,其通径的两端与顶点连成的三角形的面积为4.则此抛物线的方程是( )
| A. | y2=8$\sqrt{2}$x | B. | y2=±4$\sqrt{2}$x | C. | y2=±4x | D. | y2=±8$\sqrt{2}$x |