题目内容
3.已知△ABC中,a=2,B=45°,cosA=$\frac{3}{5}$,求b.分析 利用同角三角函数关系,可得sinA=$\frac{4}{5}$,由正弦定理可求b.
解答 解:∵cosA=$\frac{3}{5}$,
∴sinA=$\frac{4}{5}$,
由正弦定理可得$\frac{2}{\frac{4}{5}}$=$\frac{b}{\frac{\sqrt{2}}{2}}$,∴b=$\frac{5\sqrt{2}}{4}$.
点评 本题考查同角三角函数关系,正弦定理,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.函数f(x)=sin(x+$\frac{π}{3}$)+sin(x-$\frac{π}{3}$)的最大值是( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
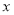 的方程
的方程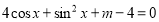 恒有实数解,则实数
恒有实数解,则实数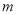 的取值范围是( )
的取值范围是( )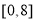 B.
B. 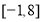 C.
C.  D.
D. 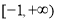
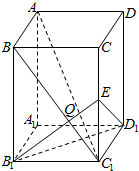 如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.
如图,长方体AC1中,已知AB=BC=a,BB1=b(b>a),连结BC1,过B1作B1E⊥BC1交CC1于E,交BC1于Q.