题目内容
15.已知 f(x)=$\frac{a-{2}^{x}}{1+{2}^{x}}$(a∈R)是奇函数,且实数k满足f(2k-1)<$\frac{1}{3}$,则k的取值范围是( )| A. | (0,+∞) | B. | (-∞,0) | C. | (-∞,1) | D. | (1,+∞) |
分析 由题意f(0)=0,求出a=1,确定f(x)=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-1+$\frac{2}{1+{2}^{x}}$,单调递减,利用f(2k-1)<$\frac{1}{3}$,f(-1)=$\frac{1}{3}$,即可求出k的取值范围.
解答 解:由题意f(0)=0,∴a=1,∴f(x)=$\frac{1-{2}^{x}}{1+{2}^{x}}$=-1+$\frac{2}{1+{2}^{x}}$,单调递减,
∵f(2k-1)<$\frac{1}{3}$,f(-1)=$\frac{1}{3}$,
∴2k-1>-1,∴k>0.
故选A.
点评 本题考查函数的奇偶性、单调性,考查不等式的解法,确定函数的单调性是关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
10.不共线的非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{b}$|=|-2$\overrightarrow{a}$|,则向量2$\overrightarrow{a}$+$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
7.已知函数f(x)=$\left\{\begin{array}{l}4\;|{\;{{log}_2}x\;}|\;\;\;\;\;0<x<2\\ \frac{1}{2}{x^2}-5x+12\;\;\;\;\;x≥2\end{array}$,若存在实数a,b,c,d满足f(a)=f(b)=f(c)=f(d),若d>c>b>a>0,则abc(d-4)的取值范围是( )
| A. | (8,9) | B. | (8,9] | C. | (12,32) | D. | [12,32) |
4.若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x)<0的解集是( )
| A. | (-1,0) | B. | (-∞,-1)∪(0,1) | C. | (-1,1) | D. | (0,1) |
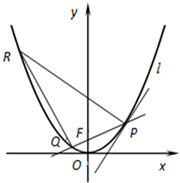 如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.
如图,点F是抛物线C:x2=2y的焦点,点P(x1,y1)为抛物线上的动点(P在第一象限),直线PF交抛物线C于另一点Q,直线l与抛物线C相切于点P.过点P作直线l的垂线交抛物线C于点R.