题目内容
1.若向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2)则$\overrightarrow{a}$-$\overrightarrow{b}$的坐标为( )| A. | (1,5) | B. | (1,1) | C. | (3,1) | D. | (3,5) |
分析 直接利用向量的坐标运算求解即可.
解答 解:向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2)则$\overrightarrow{a}$-$\overrightarrow{b}$=(3,1).
故选:C.
点评 本题考查向量的坐标运算,是基础题.

练习册系列答案
相关题目
11.直线l1:3mx+8y+3m-10=0过定点( )
| A. | (-1,-$\frac{4}{5}$) | B. | (-1,$\frac{4}{5}$) | C. | (-1,$\frac{5}{4}$) | D. | (-1,-$\frac{5}{4}$) |
12.如图,在正方体ABCD-A1B1C1D1中,M为棱D1C1的中点.设AM与平面BB1D1D的交点为O,则( )
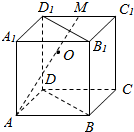

| A. | 三点D1,O,B共线,且OB=2OD1 | B. | 三点D1,O,B不共线,且OB=2OD1 | ||
| C. | 三点D1,O,B共线,且OB=OD1 | D. | 三点D1,O,B不共线,且OB=OD1 |
6.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1$(a>0)的一条渐近线方程为y=2x,则a的值为( )
| A. | $\frac{3}{2}$ | B. | $3\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | 6 |
13.从自然数1,2,3,4,5中,任意取出两个数组成两位的自然数,则在两位自然数中取出的数恰好能被3整除的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
11.已知向量$\overrightarrow{OA}$在基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}下的坐标为(8,6,4),其中$\overrightarrow{a}$=$\overrightarrow{i}$+$\overrightarrow{j}$,$\overrightarrow{b}$=$\overrightarrow{j}$+$\overline{k}$,$\overrightarrow{c}$=$\overrightarrow{k}$+$\overrightarrow{i}$则向量$\overrightarrow{OA}$在基底($\overrightarrow{i}$,$\overrightarrow{j}$,$\overrightarrow{k}$)下的坐标为( )
| A. | (12,14,10) | B. | (10,12,14) | C. | (14,12,10) | D. | (4,3,2) |