题目内容
6.若双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1$(a>0)的一条渐近线方程为y=2x,则a的值为( )| A. | $\frac{3}{2}$ | B. | $3\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | 6 |
分析 求出双曲线的渐近线方程,即可得到结果.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1$(a>0)的渐近线方程为:y=±$\frac{3}{a}x$,又双曲线$\frac{x^2}{a^2}-\frac{y^2}{9}=1$(a>0)的一条渐近线方程为y=2x,可得a=$\frac{3}{2}$.
故选:A.
点评 本题考查双曲线的简单性质的应用,是基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
16.如图所示,程序框图(算法流程图)的输出结果是( )


| A. | -2 | B. | 0 | C. | =-1 | D. | -3 |
14.已知a,b为实数,则“a+b≤2”是“a≤1且b≤1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.若向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2)则$\overrightarrow{a}$-$\overrightarrow{b}$的坐标为( )
| A. | (1,5) | B. | (1,1) | C. | (3,1) | D. | (3,5) |
11.设变量x,y满足约束条件$\left\{\begin{array}{l}2x+y≥4\\ x-y≤4\\ x-2y≥2\end{array}\right.$,则目标函数z=x+y-3的最小值为( )
| A. | -2 | B. | $-\frac{5}{3}$ | C. | -1 | D. | 5 |
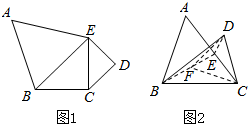 如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.
如图1,平面五边形ABCDE中,△ABE是边长为2的正三角形,△BCE、△CDE均为等腰直角三角形,且∠BCE和∠CDE为直角,现将△ABE、△CDE分别沿BE、CE折起,使平面ABE⊥平面BCE,平面DCE⊥平面BCE,如图2所示.