题目内容
14.已知点A(2,3,5),点B(3,1,4),那么A,B两点间的距离为$\sqrt{6}$.分析 利用两点间距离公式求解.
解答 解:∵点A(2,3,5),点B(3,1,4),
∴A,B两点间的距离:|AB|=$\sqrt{(3-2)^{2}+(1-3)^{2}+(4-5)^{2}}$=$\sqrt{6}$.
故答案为:$\sqrt{6}$.
点评 本题考查两点间距离的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
3.函数y=tan4x的最小正周期为( )
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
4.已知点P(1,$\frac{3}{2}$)是椭圆$\frac{x^2}{4}$+$\frac{y^2}{3}$=1上一点,点A,B是椭圆上两个动点,满足$\overrightarrow{PA}$+$\overrightarrow{PB}$=3$\overrightarrow{PO}$,则直线AB的斜率为( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
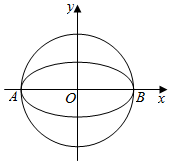 如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上.
如图,椭圆$W:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,其左顶点A在圆O:x2+y2=16上. 如图,棱柱ABCD-A1B1C1D1的底面是菱形,∠DAB=60°,AA1⊥面ABCD,且AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,棱柱ABCD-A1B1C1D1的底面是菱形,∠DAB=60°,AA1⊥面ABCD,且AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.