题目内容
5.若直线$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0)过点(1,1),则a+b的最小值等于4.分析 直线$\frac{x}{a}+\frac{y}{b}=1(a>0,b>0)$过点(1,1),$\frac{1}{a}$+$\frac{1}{b}$=1.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵直线$\frac{x}{a}+\frac{y}{b}=1(a>0,b>0)$过点(1,1),
∴$\frac{1}{a}$+$\frac{1}{b}$=1.
则a+b=(a+b)$(\frac{1}{a}+\frac{1}{b})$=2+$\frac{b}{a}$+$\frac{a}{b}$≥2+$2\sqrt{\frac{b}{a}×\frac{a}{b}}$=4,当且仅当a=b=2时取等号.
故答案为:4.
点评 本题考查了“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
17.已知命题p为真命题,命题q为假命题,则以下命题为真命题的是( )
| A. | ¬p或q | B. | p且q | C. | p或q | D. | ¬p且¬q |
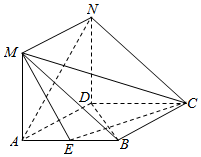 在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点. 在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC上的动点,且AE=BF.
在棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是棱AB和BC上的动点,且AE=BF.