题目内容
设C1：
-
=1，C2：
-
=1，C3：
-
=1，a2≠b2，则（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| a2 |
| x2 |
| b2 |
| y2 |
| a2 |
| A、C1和C2有公共焦点 |
| B、C1和C3有公共焦点 |
| C、C3和C2有公共渐近线 |
| D、C1和C3有公共渐近线 |
考点：双曲线的标准方程,双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据方程分别求出渐近线，焦点坐标，判断即可．
解答：
解：c=
，a2≠b2，
C1：
-
=1的焦点为（±c，0），渐近线方程为y=±
，
C2：
-
=1的焦点为（0，±c，），渐近线方程为y=±
，
C3：
-
=1的焦点为（±c，0），渐近线方程为y=±
，
∴C1，C2有公共渐近线，C1，C3有公共的焦点，
故选：B
| a2+b2 |
C1：
| x2 |
| a2 |
| y2 |
| b2 |
| bx |
| a |
C2：
| y2 |
| b2 |
| x2 |
| a2 |
| bx |
| a |
C3：
| x2 |
| b2 |
| y2 |
| a2 |
| ax |
| b |
∴C1，C2有公共渐近线，C1，C3有公共的焦点，
故选：B
点评：本题考查了双曲线的方程的运用，几何性质，关键看方程的结构形式，属于容易题．
练习册系列答案
小学夺冠AB卷系列答案
ABC考王全优卷系列答案
相关题目
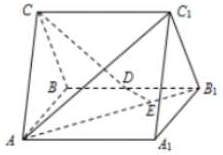如图，直三棱柱ABC-A1B1C1中，AC=BC，C到AB的距离大于1，AA1=AB=2，D为BB1的中点，E为AB1上的一点，AE=3EB1．