题目内容
9.已知椭圆x2+my2=1的焦距为$\sqrt{3}$,则m=4或$\frac{4}{7}$.分析 根据题意,将椭圆的方程变形为标准方程,求出m的范围,分2种情况讨论:①、0<m<1时,②、m>1时,每种情况下分析焦点位置,用m表示焦距,即可得关于m的值,综合两种情况即可得答案.
解答 解:根据题意,椭圆的方程为:x2+my2=1,其标准方程为$\frac{{x}^{2}}{1}$+$\frac{{y}^{2}}{\frac{1}{m}}$=1,若其表示椭圆,必有m>0且m≠1,
分2种情况讨论:
①、0<m<1时,$\frac{1}{m}$>1,椭圆的焦点在y轴上,
则c=$\sqrt{\frac{1}{m}-1}$,
若其焦距为$\sqrt{3}$,则有2$\sqrt{\frac{1}{m}-1}$=$\sqrt{3}$,
解可得m=$\frac{4}{7}$,
②、m>1时,0<$\frac{1}{m}$<1,椭圆的焦点在x轴上,
则c=$\sqrt{1-\frac{1}{m}}$,
若其焦距为$\sqrt{3}$,则有2$\sqrt{1-\frac{1}{m}}$=$\sqrt{3}$,
解可得m=4;
综合可得:m=4或m=$\frac{4}{7}$;
故答案为:4或$\frac{4}{7}$.
点评 本题考查椭圆的标准方程,注意椭圆的焦距是2c,其次要分析椭圆的焦点位置.

练习册系列答案
相关题目
 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3. 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°,E是PD的中点.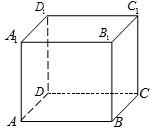 在正方体ABCD-A1B1C1D1中,给出下列结论:
在正方体ABCD-A1B1C1D1中,给出下列结论: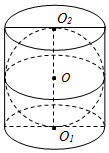 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.
如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1,球O的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$的值是$\frac{3}{2}$.