题目内容
已知数列:
,
,
,
,
,
,
,
,
,
,…依它的前10项的规律,这个数列的第2014项a2014= .
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
考点:归纳推理
专题:规律型
分析:观察数列的特征,得出它的项数是1+2+3+…+k=
(k∈N*),在每一个k段内是k个分数(k∈N*,k≥3),且它们的分子分母和为k+1;进而求出第2014项即可.
| k(k+1) |
| 2 |
解答:
解:观察数列:
,
,
,
,
,
,
,
,
,
,…,
得出:它的项数是1+2+3+…+k=
(k∈N*),
并且在每一个k段内,是k个分数(k∈N*,k≥3),且它们的分子分母和为k+1(k∈N*,k≥3);
由k=62时,
=1953<2014(k∈N*),
由k=63时,
=2016>2014(k∈N*),
故a2014在63段中
∴该数列的第2014项a2014为第63组的第61项,
故a2014=
,
故答案为:
.
| 1 |
| 1 |
| 2 |
| 1 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| 4 |
得出:它的项数是1+2+3+…+k=
| k(k+1) |
| 2 |
并且在每一个k段内,是k个分数(k∈N*,k≥3),且它们的分子分母和为k+1(k∈N*,k≥3);
由k=62时,
| k(k+1) |
| 2 |
由k=63时,
| k(k+1) |
| 2 |
故a2014在63段中
∴该数列的第2014项a2014为第63组的第61项,
故a2014=
| 3 |
| 61 |
故答案为:
| 3 |
| 61 |
点评:本题考查了数列的应用问题,解题时应根据数列的特征,总结出规律,得出正确的结论,是基础题.

练习册系列答案
相关题目
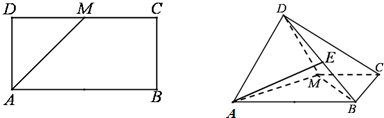 如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
如图,已知矩形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.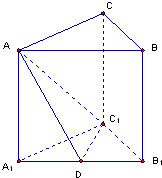 如图,直三棱柱ABC-A1B1C1底面是等腰三角形(侧棱垂直于底面的棱柱叫直棱柱),A1C1=C1B1,D是线段A1B1的中点.
如图,直三棱柱ABC-A1B1C1底面是等腰三角形(侧棱垂直于底面的棱柱叫直棱柱),A1C1=C1B1,D是线段A1B1的中点.