Question

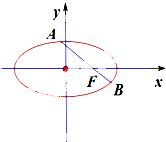如图，在平面直角坐标系xoy中，椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的离心率为

1

2

，过椭圆焦点F作弦AB．当直线AB斜率为0时，弦AB长4．
（1）求椭圆的方程； 
（2）若|AB|=

60

19

．求直线AB的方程．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程

分析：（1）由题意知e=

c

a

=

1

2

，2a=4，又a²=b²+c²，联立即可解出．
（2）设直线AB的方程为y=k（x-1），将直线AB方程代入椭圆方程中并整理得（3-4k²）x²-8k²x+4k²-12=0，
利用根与系数的关系、弦长公式即可得出．

解答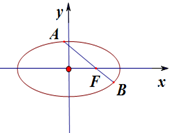： 解：（1）由题意知e=

c

a

=

1

2

，2a=4，
又a²=b²+c²，解得：a=2，b=

3

，
∴椭圆方程为：

x2

4

+

y2

3

=1．
（2）设直线AB的方程为y=k（x-1），
将直线AB方程代入椭圆方程中并整理得（3+4k²）x²-8k²x+4k²-12=0，
则x1+x2=

8k2

3+4k2

，x1•x2=

4k2-12

3+4k2

，
∴|AB|=

k2+1

|x1-x2|=

12(k2+1)

3+4k2

=|AB|=

60

19

．
解得k=±2，
∴直线AB方程为2x-y-2=0或2x+y-2=0．

点评：本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式，考查了推理能力与计算能力，属于中档题．