题目内容
下列说法:
①函数y=(
)x的反函数是y=-log2x;
②若函数f(x)满足f(x+1)=2x,则f(x)=2x+2;
③若函数f(x)的定义域是[-1,3],则函数f(2x-1)的定义域是[0,2];
④不等式log2(x+1)>log2(2x-3)的解集是(-∞,4),
其中正确的是 .
①函数y=(
| 1 |
| 2 |
②若函数f(x)满足f(x+1)=2x,则f(x)=2x+2;
③若函数f(x)的定义域是[-1,3],则函数f(2x-1)的定义域是[0,2];
④不等式log2(x+1)>log2(2x-3)的解集是(-∞,4),
其中正确的是
考点:命题的真假判断与应用
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由反函数的求法即可判断①;由换元法即可求出f(x)的表达式,即可判断②;
由函数的定义域的定义,即可求出所求的定义域,即可判断③;
运用对数函数的性质,得到x+1>2x-3>0,解出即可判断④.
由函数的定义域的定义,即可求出所求的定义域,即可判断③;
运用对数函数的性质,得到x+1>2x-3>0,解出即可判断④.
解答:
解:对于①,函数y=(
)x的反函数为y=log
x,即为y=-log2x,故①对;
对于②,若函数f(x)满足f(x+1)=2x,则f(x)=2x-2,故②错;
对于③,令2x-1=t,则-1≤t≤3,解得0≤x≤2,故③对;
对于④,由x+1>2x-3>0,解得
<x<4,故④错.
故答案为:①③
| 1 |
| 2 |
| 1 |
| 2 |
对于②,若函数f(x)满足f(x+1)=2x,则f(x)=2x-2,故②错;
对于③,令2x-1=t,则-1≤t≤3,解得0≤x≤2,故③对;
对于④,由x+1>2x-3>0,解得
| 3 |
| 2 |
故答案为:①③
点评:本题考查函数的反函数的求法、函数的解析式的求法和函数的定义域的求法,考查对数不等式的解法,属于基础题和易错题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目

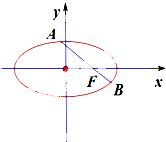 如图,在平面直角坐标系xoy中,椭圆
如图,在平面直角坐标系xoy中,椭圆