题目内容
若点A(a,b)在第一象限,且在直线x+y-1=0上,则
+
的最小值为( )
| 1 |
| a |
| 4 |
| b |
| A、8 | B、9 | C、10 | D、12 |
考点:基本不等式在最值问题中的应用
专题:不等式的解法及应用
分析:根据点A(a,b)在第一象限,且在直线x+y-1=0上,可得a+b=1,且a>0,b>0,利用“1”的代换,结合基本不等式,即可得出结论.
解答:
解:∵点A(a,b)在第一象限,且在直线x+y-1=0上,
∴a+b=1,且a>0,b>0,
∴
+
=(a+b)(
+
)=5+
+
≥5+2
=9,
当且仅当
=
,即a=
,b=
时,
+
的最小值为9.
故选B.
∴a+b=1,且a>0,b>0,
∴
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
|
当且仅当
| b |
| a |
| 4a |
| b |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| a |
| 4 |
| b |
故选B.
点评:本题考查基本不等式的运用,考查“1”的代换,确定a+b=1,且a>0,b>0是关键.

练习册系列答案
相关题目
实数x,y满足x+y-4=0,则 x2+y2的最小值是( )
| A、8 | ||
| B、4 | ||
C、2
| ||
| D、2 |
函数y=
+x(x>3)的最小值为( )
| 1 |
| x-3 |
| A、4 | B、3 | C、2 | D、5 |
若角α的终边过点P(3,-4),则cosα等于( )
A、
| ||
B、-
| ||
C、-
| ||
D、
|
已知函数f(x)=
,若f(a)+f(2)=0,则实数a的值等于( )
|
| A、-7 | B、-5 | C、-1 | D、-3 |
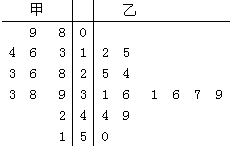 已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )
已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图(如图所示),则( )| A、甲篮球运动员比赛得分更稳定,中位数为26 |
| B、甲篮球运动员比赛得分更稳定,中位数为27 |
| C、乙篮球运动员比赛得分更稳定,中位数为31 |
| D、乙篮球运动员比赛得分更稳定,中位数为36 |