题目内容

一个袋子中有号码为1、2、3、4、5大小相同的5个小球，现从袋中任意取出一个球，取出后不放回，然后再从袋中任取一个球，则第一次取得号码为奇数，第二次取得号码为偶数球的概率为（　　）
A、
3
5
B、
4
5
C、
3
20
D、
3
10
考点：列举法计算基本事件数及事件发生的概率
专题：概率与统计
分析：先求出第一次取得号码为奇数的概率，再求出第二次取得号码为偶数球的概率，根据概率公式计算即可．
解答： 解：1、2、3、4、5大小相同的5个小球，从袋中任取一个球，则第一次取得号码为奇数的概率为
3
5
，
第二次取得号码为偶数球的概率为
2
4
=
1
2
，
故第一次取得号码为奇数，第二次取得号码为偶数球的概率为
3
5
×
1
2
=
3
10
，
故选：D．
点评：本题考查了条件概率的求法，属于基础题．
练习册系列答案
相关题目
已知平面α经过点A（3，1，-1），B（1，-1，0）且平行于向量
a
=（-1，0，2），求平面α的一个法向量．
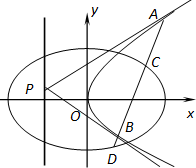已知中心在原点的椭圆Γ1和抛物线Γ2有相同的焦点（1，0），椭圆Γ1的离心率为
1
2
，抛物线Γ2的顶点为原点．
（Ⅰ） 求椭圆Γ1和抛物线Γ2的方程；
（Ⅱ） 设点P为抛物线Γ2准线上的任意一点，过点P作抛物线Γ2的两条切线PA，PB，其中A，B为切点．
（ⅰ）设直线PA，PB的斜率分别为k1，k2，求证：k1k2为定值；
（ⅱ）若直线AB交椭圆Γ1于C，D两点，S△PAB，S△PCD分别是△PAB，△PCD的面积，试问：
S△PAB
S△PCD
是否有最小值？若有，求出最小值；若没有，请说明理由．
已知数列{an}中．a1=1，anan+1=（
1
2
）n（n∈N*）
（1）求证：数列{a2n}与{a2n-1}（n∈N*）都是等比数列
（2）若数列{an}的前2n项的和为T2n，令bn=（3-T2n）•n（n+1），求数列{bn}的最大项．
已知函数f（x）=
1-x
+
1+x
，若x，y满足f（x+1）-f（y）＞0，则x2+y2-2x+1的取值范围是
 
．
已知某个几何体的三视图如图所示，根据图中的数据，计算该几何体的表面积和体积．
对任意x，y∈R，|x-1|+|x|+|y-1|+|x+1|的最小值为
 
．
已知数列{an}中，a1=1，a2=
1
4
，且an+1=
(n-1)an
n-an
（n=2，3，4…）．
（1）求数列{an}的通项公式；
（2）求证：对一切n∈N*，有
n
k=1
ak2＜
7
6
．
已知函数f（x）=sinωx+
3
cosωx的最小正周期为π，x∈R，ω＞0是常数．
（1）求ω的值；
（2）若f（
θ
2
+
π
12
）=
6
5
，θ∈（0，
π
2
），求sin2θ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网