题目内容
9.已知函数f(x)=(a-$\frac{1}{2}$)x2+lnx(a∈R).(I)若函数f(x)在点(1,f(1))处的切线方程为2x+y+b=0,求a,b的值;
(II)若在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方,求a的取值范围.
分析 (I)由题知,$f'(x)=(2a-1)x+\frac{1}{x}$,又f'(1)=-2,从而求出a=-1,由此能求出b=$\frac{1}{2}$.
(II)令$g(x)=f(x)-2ax=(a-\frac{1}{2}){x^2}-2ax+lnx$,则g(x)的定义域为(0,+∞).在区间(1,+∞)上函数f(x)的图象恒在直线y=2ax下方等价于g(x)<0在区间(1,+∞)上恒成立.由此利用导数性质能求出a的取值范围.
解答 (本小题满分12分)
解:(I)∵f(x)=(a-$\frac{1}{2}$)x2+lnx(a∈R),
∴由题知,$f'(x)=(2a-1)x+\frac{1}{x}$,…(1分)
又f'(1)=-2,即2a=-2,∴a=-1.…(2分)
∴$f(x)=-\frac{3}{2}{x^2}+lnx$,∴$f(1)=-\frac{3}{2}$.
∴切点为$(1,-\frac{3}{2})$,代入切线方程得:$2×1-\frac{3}{2}+b=0$,
解得b=$\frac{1}{2}$.
∴a=-1,$b=-\frac{1}{2}$.…(4分)
(II)令$g(x)=f(x)-2ax=(a-\frac{1}{2}){x^2}-2ax+lnx$,则g(x)的定义域为(0,+∞).
在区间(1,+∞)上函数f(x)的图象恒在直线y=2ax下方
等价于g(x)<0在区间(1,+∞)上恒成立.
∵$g'(x)=(2a-1)x-2a+\frac{1}{x}=\frac{{(2a-1){x^2}-2ax+1}}{x}=\frac{(x-1)[(2a-1)x-1]}{x}$,…(5分)
令g'(x)=0,得x1=1或${x_2}=\frac{1}{2a-1}$.…(6分)
①若$\frac{1}{2}<a<1$,则$\frac{1}{2a-1}>1$.
∴在$(\frac{1}{2a-1},+∞)$上有g'(x)>0,在$(1,\frac{1}{2a-1})$上有g'(x)<0.
∴g(x)在$(1,\frac{1}{2a-1})$上递减,在$(\frac{1}{2a-1},+∞)$上递增.
∴$g(x)≥g(\frac{1}{2a-1})$,
∴与g(x)<0在区间(1,+∞)上恒成立相背,不符合题意.…(8分)
②若a≥1时,则$0<\frac{1}{2a-1}≤1$,∵在(1,+∞)上有g'(x)>0,
∴g(x)在区间(1,+∞)递增.
∴g(x)≥g(1),∴不符合题意.…(10分)
③若$a≤\frac{1}{2}$,则2a-1≤0,∵在区间(1,+∞)上有g'(x)<0,则g(x)在区间(1,+∞)递减.
∴g(x)<g(1)在(1,+∞)恒成立,要使g(x)<0在(1,+∞)恒成立,
只需$g(1)=-a•\frac{1}{2}≤0$.∴$a≥-\frac{1}{2}$,∴$-\frac{1}{2}≤a≤\frac{1}{2}$.
综上,当$a∈[-\frac{1}{2},\frac{1}{2}]$时,函数f(x)的图象恒在直线y=2ax下方.…(12分)
点评 本题考查实数值的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | (1,+∞) | B. | $(0,\frac{3}{4})$ | C. | $[\frac{3}{4},\frac{4}{3})$ | D. | $[\frac{3}{4},+∞)$ |
| A. | (x-2)5 | B. | (x+1)5 | ||
| C. | x5 | D. | x5+5x4+10x3+10x2+5x+1 |
 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
 如图,过圆内接四边形ABCD的顶点C引切线MN,AB为圆的直径.
如图,过圆内接四边形ABCD的顶点C引切线MN,AB为圆的直径.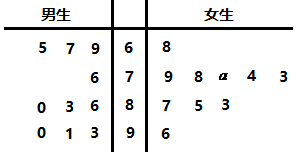 某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).
某中学为了普及法律知识,举行了一次法律知识竞赛活动.下面的茎叶图记录了男生、女生各10名学生在该次竞赛活动中的成绩(单位:分).