题目内容
9.(重点中学做)设实数x,y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$,则 z=x2+y2的取值范围是( )| A. | [2,2$\sqrt{5}$] | B. | [10,20] | C. | [4,20] | D. | [$\frac{18}{5}$,20] |
分析 由约束条件作出平面区域,数形结合得到最优解,联立方程组求出最优解的坐标,由z=x2+y2的几何意义得答案.
解答  解:由约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+3y-6≥0}\\{y-2≤0}\end{array}\right.$作出可行域如图,
由图可知,可行域内的点到原点距离的最小值为d=$\frac{|-6|}{\sqrt{{1}^{2}+{3}^{2}}}=\frac{6\sqrt{10}}{10}=\frac{3\sqrt{10}}{5}$,
联立$\left\{\begin{array}{l}{y=2}\\{x-y-2=0}\end{array}\right.$,得A(4,2),
|OA|=$\sqrt{{4}^{2}+{2}^{2}}=2\sqrt{5}$,
∴z=x2+y2的取值范围是:[$\frac{18}{5},20$].
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
 已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )
已知正四棱锥的底面边长为2a,其侧视图是腰长为2的等腰三角形(如图所示),当正视图的面积最大时,该正四棱锥的表面积为( )| A. | 8 | B. | 8+8$\sqrt{2}$ | C. | 8$\sqrt{2}$ | D. | 4+8$\sqrt{2}$ |
19.阅读如图所示的程序框图,运行相应的程序,输出S的值为( )


| A. | 8 | B. | 32 | C. | 48 | D. | 384 |
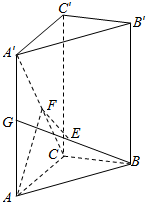 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
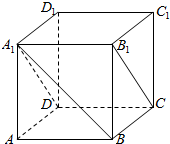 (1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.
(1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明. 某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:
某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长: