题目内容
18.若$\overrightarrow{a}$,$\overrightarrow{b}$为非零向量,求证:||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,并说明取等号的条件.分析 分向量共线与不共线的情况,利用向量加法、减法的三角形法则做出图形,结合三角形的边的关系:“两边之和大于第三边,两边之差小于第三边”进行证明.
解答 证明:分三种情况考虑.
(1)当a、b共线且方向相同时,|a|-|b|<|a+b|=|a|+|b|,|a|-|b|=|a-b|<|a|+|b|.
(2)当a、b共线且方向相反时,
∵a-b=a+(-b),a+b=a-(-b),
利用(1)的结论有||a|-|b||<|a+b|<|a|+|b|,|a|-|b|<|a-b|=|a|+|b|.
(3)当a,b不共线时,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,作$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$=a+b,$\overrightarrow{BA}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$=a-b,
利用三角形两边之和大于第三边,两边之差小于第三边,得||a|-|b||<|a±b|<|a|+|b|.
综上得证.
点评 本题主要考查了平面向量的共线与不共线时两向量和(或差)的模与向量模的和(或差)的大小关系,解决问题的关键是要熟练运用向量的加法及减法的三角形法则(平行四边形法则).分类讨论的数学思想要注意掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.函数f(x)=2cos2(x+$\frac{π}{8}$)-2sin(x+$\frac{π}{8}$)cos(x+$\frac{π}{8}$)-1的最大值是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}$ |
7.若函数f(x)=x2log2(x+$\sqrt{x^2+m}$)为奇函数,则m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
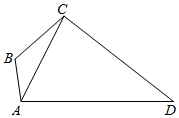 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.