题目内容
8.已知集合B={1},C={3},A∪B={1,2},则( )| A. | A∩B=∅ | B. | A∩C=∅ | C. | A∪C={1,2,3} | D. | A∪C={2,3} |
分析 求出集合A中的元素,从而求出A∩B即可.
解答 解:集合B={1},C={3},
A∪B={1,2},
∴A={2}或A={1,2},
∴A∩C=∅,
故选:B.
点评 本题考查了集合的运算性质,是一道基础题.

练习册系列答案
相关题目
7.若函数f(x)=x2log2(x+$\sqrt{x^2+m}$)为奇函数,则m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知圆(x-m)2+y2=4上存在两点关于直线x-y-2=0对称,若离心率为$\sqrt{2}$的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线与圆相交,则它们的交点构成的图形的面积为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4 |
13.下列函数中满足$f(\frac{{{x_1}+{x_2}}}{2})<\frac{{f({x_1})+f({x_2})}}{2}({x_1}≠{x_2})$的是( )
| A. | f(x)=3x+2 | B. | $f(x)=\sqrt{x}$ | C. | $f(x)=-{(\frac{1}{2})^x}$ | D. | f(x)=x2+x+1 |
20.已知集合A={0,1,2},B={y|y=2x,x∈A},则A∪B中的元素个数为( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
18.下列函数中,既是偶函数又存在零点的是( )
| A. | y=x2+1 | B. | y=2|x| | C. | y=lnx | D. | y=cosx |
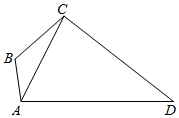 如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.
如图,在平面四边形ABCD中,AB⊥AD,AB=1,AC=$\sqrt{7}$,∠ABC=$\frac{2π}{3}$,∠ACD=$\frac{π}{3}$.