题目内容
3.已知f(x)=ax3+b3$\sqrt{x}$+4(a,b∈R),f[lg(log32)]=1,则f[lg(log23)]的值为( )| A. | -1 | B. | 3 | C. | 7 | D. | 8 |
分析 易判lg(log23)与lg(log32)互为相反数,构造函数f(x)=g(x)+4,即g(x)=ax3+b3$\sqrt{x}$,利用g(x)的奇偶性可求结果.
解答 解:∵lg(log23)+lg( log32)=lg(log23•log32)=lg1=0,
∴lg(log23)与lg(log32)互为相反数,
令f(x)=g(x)+4,即g(x)=ax3+b3$\sqrt{x}$,易知g(x)为奇函数,
则g(lg(log23))+g(lg( log32))=0,
∴f(lg(log23))+f(lg( log32))=g(lg(log23))+4+g(lg( log32))+4=8,
又f(lg(log23))=1,∴f(lg( log32))=7,
故选:C.
点评 本题考查函数奇偶性的应用,解决本题的关键细心观察自变量的相反关系,然后灵活构造函数,借助函数的奇偶性求解.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
13.从个位数与十位数之和为偶数的两位数中任取一个,其中个位数为2或3的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
14.已知AB为圆x2+y2=1的一条直径,点P为直线x-y+2=0上任意一点,则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
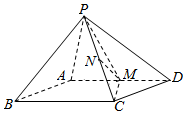 如图,四棱锥的底面ABCD是平行四边形,PA⊥平面ABCD,M是AD中点,N是PC中点.
如图,四棱锥的底面ABCD是平行四边形,PA⊥平面ABCD,M是AD中点,N是PC中点.