题目内容
15．已知函数f（x）=$\sqrt{3}$sin$\frac{π}{t}$x，若存在f（x）的两个相邻的最值点，x1，x2满足（x1-x2）2-2[f（x1）]2-2[f（x2）]2＜t，则实数t的取值范围是（0，1）．分析 不妨设x2＞x1，f（x1）=$\sqrt{3}$，f（x2）=-$\sqrt{3}$，由题意可得t2＜t，从而求得t的范围．
解答 解：不妨设x2＞x1，f（x1）=$\sqrt{3}$，f（x2）=-$\sqrt{3}$，
由题意可得 x2-x1 =$\frac{1}{2}$•$\frac{2π}{\frac{π}{t}}$=t．
由（x1-x2）2-2[f（x1）]2-2[f（x2）]2＜t，可得t2-2（3-3）＜t，
解得0＜t＜1，
故答案为：（0，1）．
点评 本题主要考查正弦函数的图象特征，正弦函数的周期性和最值，属于中档题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
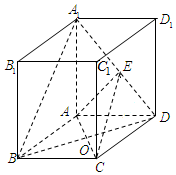如图，四棱柱ABCD-A1B1C1D1中，底面四边形ABCD为菱形，∠ABC=60°，AA1=AC=2，A1B=A1D=2$\sqrt{2}$，点E在线段A1D上．
10．在复平面内，复数$\frac{2+i}{2i}$对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
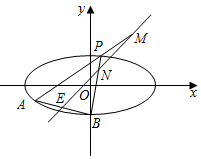如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞b＞0），点B是其下顶点，直线x+3y+6=0与椭圆C交于A，B两点（点A在x轴下方），且线段AB的中点E在直线y=x上．