题目内容
8.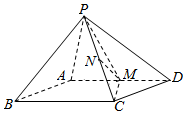 如图,四棱锥的底面ABCD是平行四边形,PA⊥平面ABCD,M是AD中点,N是PC中点.
如图,四棱锥的底面ABCD是平行四边形,PA⊥平面ABCD,M是AD中点,N是PC中点.(1)求证:MN∥面PAB;
(2)若平面PMC⊥平面PAD,求证CM⊥AD.
分析 (1)取BC中点E,连结ME、NE,由已知推导出平面PAB∥平面MNE,由此能证明MN∥平面PAB.
(2)利用面面垂直的性质,由平面PMC⊥平面PAD,平面ABCD⊥平面PAD,可证CM⊥平面PAD,由AD?平面PAD,即可证明CM⊥AD.
解答  证明:(1)取BC中点E,连结ME、NE,
证明:(1)取BC中点E,连结ME、NE,
∵四棱锥的底面ABCD是平行四边形,M是AD中点,N是PC中点,
∴ME∥AB,NE∥PB,
∵AB∩PB=B,ME∩NE=E,
∴平面PAB∥平面MNE,
∵MN?平面MNE,
∴MN∥平面PAB.
(2)∵平面PMC⊥平面PAD,
∵PA⊥平面ABCD,PA?平面PAD,
∴平面ABCD⊥平面PAD,
又∵平面PMC∩平面ABCD=CM,
∴CM⊥平面PAD,
∵AD?平面PAD,
∴CM⊥AD.
点评 本题主要考查了线面平行的证明,考查了面面垂直的性质,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
19.已知a,b∈R,则“$\sqrt{a-1}>\sqrt{b-1}$”是“logab<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.在正方体ABCD-A1B1C1D1中,E为棱AA1的中点,F是棱A1B1上的点,且A1F:FB1=1:3,则异面直线EF与BC1所成角的正弦值为( )
| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{15}}}{5}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
13.已知圆O:x2+y2=9;直线l过点(0,3),倾斜角为α,α在区(0,π)内随机取值,l与圆O相交于A、B两点,则|AB|≤3$\sqrt{2}$的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
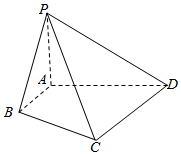 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD中,∠A=90°,AB∥CD,AB=1,AD=CD=2.