题目内容
圆C:x2+y2-8x+4y+19=0关于直线x+y+1=0对称的圆的方程为 .
考点:圆的一般方程
专题:计算题,直线与圆
分析:求出圆C:x2+y2-8x+4y+19=0关于直线x+y+1=0对称的圆的圆心,即可求出结论.
解答:
解:圆C:x2+y2-8x+4y+19=0,可化为圆C:(x-4)2+(y+2)2=1,圆心为(4,-2),半径为1,
设圆C:x2+y2-8x+4y+19=0关于直线x+y+1=0对称的圆的圆心为(a,b),则
,
∴a=1,b=-5
∴圆的方程为(x-1)2+(y+5)2=1.
故答案为:(x-1)2+(y+5)2=1.
设圆C:x2+y2-8x+4y+19=0关于直线x+y+1=0对称的圆的圆心为(a,b),则
|
∴a=1,b=-5
∴圆的方程为(x-1)2+(y+5)2=1.
故答案为:(x-1)2+(y+5)2=1.
点评:本题考查圆的方程,考查学生分析解决问题的能力,确定圆心的坐标是关键.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知曲线C的方程为x2-xy+y2-2=0,则下列各点中,在曲线C上的点是( )
A、(0,
| ||
| B、(1,-2) | ||
| C、(2,-3) | ||
| D、(3,8) |
已知A为圆A:(x-1)2+y2=25的圆心,平面上点P满足PA=
,那么点P与圆A的位置关系是( )
| 3 |
| A、点P在圆A上 |
| B、点P在圆A内 |
| C、点P在圆A外 |
| D、无法确定 |
抛物线y2=-16x的焦点坐标为( )
| A、(0,-4) |
| B、(4,0) |
| C、(0,4) |
| D、(-4,0) |
若幂函数y=xα在 (0,+∞)上是增函数,则α一定( )
| A、α>0 | B、α<0 |
| C、α>1 | D、不确定 |
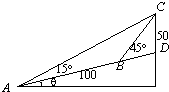 如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).
如图所示,在斜度一定的山坡上的一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100米后到达点B,又从点B测测建筑物顶端C对于山坡的斜度为45°,建筑物的高CD为50米,求此山对于地面的倾斜角θ的余弦值(结果保留最简根式).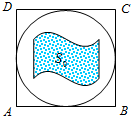 如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法:
如图,在边长为2的正方形ABCD中有一内切圆,某人为了用随机模拟的方法估计出该圆内阴影部分(旗帜)的面积S0,往正方形ABCD内随机撒了100粒品质相同 的豆子,结果有75粒落在圆内,有25粒落在阴影部分内,据此,有五种说法: