题目内容
已知
=(sinx,2
sinx),
=(2cosx,sinx)定义f(x)=
•
-
.
(1)求f(x)的解析式;
(2)写出f(x)的图象是由y=sinx的图象经过怎样的变换得到的?
| a |
| 3 |
| b |
| a |
| b |
| 3 |
(1)求f(x)的解析式;
(2)写出f(x)的图象是由y=sinx的图象经过怎样的变换得到的?
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)利用数量积运算、倍角公式、两角和差的正弦公式即可得出;
(2)由y=sinx的图象向右平移
个单位可得y=sin(x-
),再把横坐标缩短为原来的
可得y=sin(2x-
),再把纵坐标扩大为的2倍即可得出f(x)=2sin(2x-
).
(2)由y=sinx的图象向右平移
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
解答:
解:(1)f(x)=
•
-
=2sinxcosx+2
sin2x-
=sin2x-
cos2x=2sin(2x-
).
(2)由y=sinx的图象向右平移
个单位可得y=sin(x-
),再把横坐标缩短为原来的
可得y=sin(2x-
),
再把纵坐标扩大为的2倍即可得出f(x)=2sin(2x-
).
| a |
| b |
| 3 |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
(2)由y=sinx的图象向右平移
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
再把纵坐标扩大为的2倍即可得出f(x)=2sin(2x-
| π |
| 3 |
点评:本题考查了向量数量积运算、倍角公式、两角和差的正弦公式,三角函数变换,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 已知椭圆C:
已知椭圆C: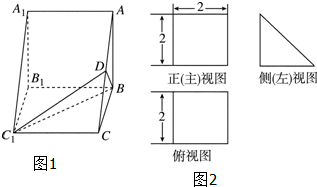 直三棱柱ABC-A1B1C1的直观图(图1)及三视图(图2)如图所示,D为AC的中点
直三棱柱ABC-A1B1C1的直观图(图1)及三视图(图2)如图所示,D为AC的中点 如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,则小正方形的边长为
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,则小正方形的边长为