题目内容
9.已知函数f(x)=$\left\{\begin{array}{l}1+{log_2}x,x≥1\\ 2x-1,x<1\end{array}\right.$,则f[f(0)+2]=1.分析 先求f(0)=-1,可得f(0)+2=1,再求f[f(0)+2],注意运用对数值的求法,即可得到所求.
解答 解:函数f(x)=$\left\{\begin{array}{l}1+{log_2}x,x≥1\\ 2x-1,x<1\end{array}\right.$,
可得f(0)=2×0-1=-1,
f(0)+2=-1+2=1,
f[f(0)+2]=f(1)=1+log21=1+0=1.
故答案为:1.
点评 本题考查分段函数值的求法,注意运用分段函数各段的解析式,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列语句可以是赋值语句的是( )
| A. | S=a+1 | B. | a+1=S | C. | S-1=a | D. | S-a=1 |
4.已知M、N是焦点为F的抛物线y2=4x上两个不同点,且线段MN的中点A的横坐标是3,直线MN与x轴交于点B,则点B的横坐标的取值范围是( )
| A. | (-3,3] | B. | (-∞,3] | C. | (-6,-3] | D. | (-6,3) |
1.椭圆$\frac{{x}^{2}}{3}$+y2=1上的点到直线x+y-4=0的最大距离是( )
| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{4\sqrt{2}-\sqrt{6}}{2}$ | D. | 2$\sqrt{2}$-1 |
19.小明同学计划两次购买同一种笔芯(两次笔芯的单价不同),有两种方案:第一种方法是每次购买笔芯数量一定:第二种方法是每次购买笔芯所花钱数一定.则哪种购买方式比较经济( )
| A. | 第一种 | B. | 第二种 | C. | 两种一样 | D. | 无法判断 |
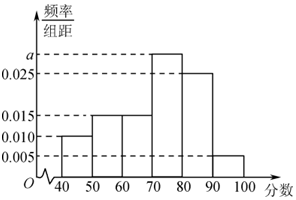 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…[90,100),后得到频率分布直方图(如图所示)
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…[90,100),后得到频率分布直方图(如图所示)