题目内容
7.在平面直角坐标系xOy中,已知点A(x1,y1),B(x2,y2)是椭圆E:$\frac{{x}^{2}}{4}$+y2=1上的非坐标轴上的点,且4kOA•KOB+1=0(kOA,kOB分别为直线OA,OB的斜率)(1)证明:x12+x22,y12+y22均为定值;
(2)判断△OAB的面积是否为定值,若是,求出该定值;若不是.请说明理由.
分析 (1)将A,B的坐标代入椭圆方程,运用直线的斜率公式,化简整理即可得到定值;
(2))△OAB的面积为S=$\frac{1}{2}$|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•sin<$\overrightarrow{OA}$,$\overrightarrow{OB}$>,由向量的数量积的定义,可得S=$\frac{1}{2}$$\sqrt{|\overrightarrow{OA}{|}^{2}•|\overrightarrow{OB}{|}^{2}-(\overrightarrow{OA}•\overrightarrow{OB})^{2}}$,运用向量的坐标运算,化简整理,即可得到定值.
解答 解:(1)证明:由题意可得$\frac{{{x}_{1}}^{2}}{4}$+y12=1,即有y12=1-$\frac{{{x}_{1}}^{2}}{4}$;
$\frac{{{x}_{2}}^{2}}{4}$+y22=1,即有y22=1-$\frac{{{x}_{2}}^{2}}{4}$.
由4kOA•KOB+1=0,可得4•$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-1,
即有16y12y22=x12x22,
即16(1-$\frac{{{x}_{1}}^{2}}{4}$)(1-$\frac{{{x}_{2}}^{2}}{4}$)=x12x22,
化简可得x12+x22=4;
y12+y22=1,则x12+x22,y12+y22均为定值;
(2)△OAB的面积为S=$\frac{1}{2}$|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•sin<$\overrightarrow{OA}$,$\overrightarrow{OB}$>
=$\frac{1}{2}$$\sqrt{|\overrightarrow{OA}{|}^{2}•|\overrightarrow{OB}{|}^{2}-(\overrightarrow{OA}•\overrightarrow{OB})^{2}}$
=$\frac{1}{2}$$\sqrt{({{x}_{1}}^{2}+{{y}_{1}}^{2})({{x}_{2}}^{2}+{{y}_{2}}^{2})-({x}_{1}{x}_{2}+{y}_{1}{y}_{2})^{2}}$
=$\frac{1}{2}$$\sqrt{{{x}_{1}}^{2}{{y}_{2}}^{2}+{{x}_{2}}^{2}{{y}_{1}}^{2}-2{x}_{1}{x}_{2}{y}_{1}{y}_{2}}$
=$\frac{1}{2}$$\sqrt{{{x}_{1}}^{2}(1-\frac{1}{4}{{x}_{2}}^{2})+{{x}_{2}}^{2}(1-\frac{1}{4}{{x}_{1}}^{2})+\frac{1}{2}{{x}_{1}}^{2}{{x}_{2}}^{2}}$
=$\frac{1}{2}$$\sqrt{{{x}_{1}}^{2}+{{x}_{2}}^{2}}$=1.
故△OAB的面积为定值1.
点评 本题考查椭圆的方程的运用,直线的斜率公式的运用和三角形的面积的求法,注意运用向量的数量积,考查化简整理的运算能力,属于中档题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案(1)求f(x)的单调增区间与减区间;
(2)填表(不要求过程,只填结果即可)
| m的范围 | |||
| 方程f(x)=0的解得个数 | 1 | 2 | 3 |
| A. | a>b>c | B. | b>c>a | C. | c>a>b | D. | c>b>a |
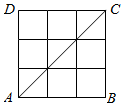 如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.
如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.