题目内容

20．函数y=sinx-1的最小值是2．

分析 根据正弦函数的值域为[-1，1]可得：当sinx取最小值-1时，函数y=sinx-1的最小值2．

解答 解：∵sinx∈[-1，1]，
∴当sinx取最小值-1时，
函数y=sinx-1的最小值是2，
故答案为：2

点评 本题考查的知识点是正弦函数的图象和性质，熟练掌握正弦函数的图象和性质，是解答的关键．

练习册系列答案
相关题目
10．函数$y=sin（\frac{2π}{3}x+\frac{π}{4}）$的最小正周期3．
11．{an}的通项公式为an=-n+p，{bn}的通项公式为${b_n}={2^{n-5}}$，设${c_n}=\left\{\begin{array}{l}{a_n}，{a_n}≤{b_n}\\{b_n}，{a_n}＞{b_n}\end{array}\right.$，若在数列{cn}中，c9＞cn，n∈N*，n≠9，则实数p的取值范围是17＜p＜26．
8．函数f（x）=ax2-2x+1，若y=f（x）在区间[-$\frac{1}{2}$，$\frac{1}{2}$]上有零点，则实数a的取值范围为（-∞，0]．
15．数列{an}满足：an-1+an+1＞2an（n＞1，n∈N*），给出下述命题：
①若数列{an}满足：a2＞a1，则an＞an-1（n＞1，n∈N*）成立；
②存在常数c，使得an＞c（n∈N*）成立；
③若p+q＞m+n（其中p，q，m，n∈N*），则ap+aq＞am+an；
④存在常数d，使得an＞a1+（n-1）d（n∈N*）都成立．
上述命题正确的①④．（写出所有正确结论的序号）
5．已知数列{an}的前n项和Sn=$\frac{1}{2}$（an+1），
（1）求数列{an}的通项公式；
（2）比较4an与Sn的大小．
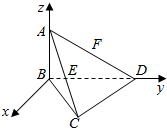12．如图点A（0，0，a），在四面体ABCD中，AB⊥平面BCD，BC=CD，∠BCD=90°，∠ADB=30°，E，F分别是AC，AD的中点，求D，C，E，F这四点的坐标．
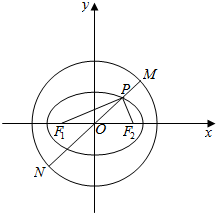9．如图，已知椭圆C：$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1，圆O：x2+y2=13，椭圆C的左右焦点分别为F1、F2，过椭圆上一点P和原点O作直线l交圆O于M，N两点，若|PF1|•|PF2|=6，则|PM|•|PN|的值为（　　）
A．7B．8C．10D．12
10．若函数y=f（x）的值域为[$\frac{1}{2}$，3]，则函数F（x）=f（x-1）+$\frac{1}{f（x-1）}$的值域是（　　）
A．[$\frac{1}{2}$，3]B．[2，$\frac{10}{3}$]C．[$\frac{5}{2}$，$\frac{10}{3}$]D．[3，$\frac{10}{3}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网