题目内容
9.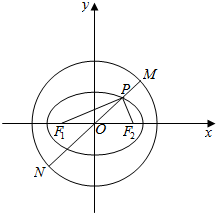 如图,已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1,圆O:x2+y2=13,椭圆C的左右焦点分别为F1、F2,过椭圆上一点P和原点O作直线l交圆O于M,N两点,若|PF1|•|PF2|=6,则|PM|•|PN|的值为( )
如图,已知椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{3}$=1,圆O:x2+y2=13,椭圆C的左右焦点分别为F1、F2,过椭圆上一点P和原点O作直线l交圆O于M,N两点,若|PF1|•|PF2|=6,则|PM|•|PN|的值为( )| A. | 7 | B. | 8 | C. | 10 | D. | 12 |
分析 由椭圆的定义及条件有$\left\{\begin{array}{l}{|P{F}_{1}|+|P{F}_{2}|=6}\\{|P{F}_{1}||P{F}_{2}|=6}\end{array}\right.$,可解出|PF1|,|PF2|,设P(x,y),且${F}_{1}(-\sqrt{6},0),{F}_{2}(\sqrt{6},0)$,从而可以求出P点的坐标$(\frac{3}{\sqrt{2}},\frac{\sqrt{3}}{\sqrt{2}})$,这样便可写出直线PO的方程,而联立圆的方程便可得出M,N的坐标,从而可以求出|PM|•|PN|的值.
解答 解:根据条件,$\left\{\begin{array}{l}{|P{F}_{1}|+|P{F}_{2}|=6}\\{|P{F}_{1}||P{F}_{2}|=6}\end{array}\right.$;
解得$|P{F}_{1}|=3+\sqrt{3},|P{F}_{2}|=3-\sqrt{3}$;
设P(x,y),则:$\left\{\begin{array}{l}{(x+\sqrt{6})^{2}+{y}^{2}=(3+\sqrt{3})^{2}}\\{(x-\sqrt{6})^{2}+{y}^{2}=(3-\sqrt{3})^{2}}\end{array}\right.$;
解得$\left\{\begin{array}{l}{x=\frac{3}{\sqrt{2}}}\\{y=\frac{\sqrt{3}}{\sqrt{2}}}\end{array}\right.$,$P(\frac{3}{\sqrt{2}},\frac{\sqrt{3}}{\sqrt{2}})$;
∴直线PO的方程为$y=\frac{\sqrt{3}}{3}x$,带入圆的方程并整理得:
${x}^{2}=\frac{39}{4}$;
∴$x=±\frac{\sqrt{39}}{2}$,y=$±\frac{\sqrt{13}}{2}$;
∴$M(\frac{\sqrt{39}}{2},\frac{\sqrt{13}}{2}),N(-\frac{\sqrt{39}}{2},-\frac{\sqrt{13}}{2})$;
∴$|PM|•|PN|=\sqrt{(\frac{3}{\sqrt{2}}-\frac{\sqrt{39}}{2})^{2}+(\frac{\sqrt{3}}{\sqrt{2}}-\frac{\sqrt{13}}{2})^{2}}$$•\sqrt{(\frac{3}{\sqrt{2}}+\frac{\sqrt{39}}{2})^{2}+(\frac{\sqrt{3}}{\sqrt{2}}+\frac{\sqrt{13}}{2})^{2}}$=$\sqrt{19-2\sqrt{78}}•\sqrt{19+2\sqrt{78}}=7$.
故选A.
点评 考查椭圆的标准方程,椭圆的定义,以及两点间距离公式,直线的点斜式方程,数形结合解题的方法.

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=0 | C. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$ | D. | $\overrightarrow{AB}$=-$\overrightarrow{BA}$ |
| A. | [$\frac{\sqrt{30}}{5}$,$\frac{\sqrt{6}}{2}$] | B. | (1,$\frac{\sqrt{6}}{2}$] | C. | (1,$\frac{\sqrt{30}}{5}$] | D. | [$\sqrt{2}$,+∞) |
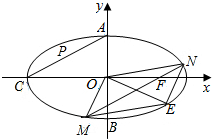 如图:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的上顶点为A,下顶点为B,左顶点为C,F为右焦点,过F作与AC平行的直线交椭圆于M、N两点.
如图:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的上顶点为A,下顶点为B,左顶点为C,F为右焦点,过F作与AC平行的直线交椭圆于M、N两点.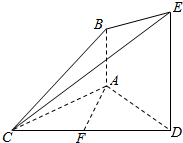 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.