题目内容
17.已知Rt△ABC中,$∠A=\frac{π}{2}$,以B,C为焦点的双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)经过点A,且与AB边交于点D,若|AD|=2|BD|,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
分析 设|BD|=t,则|AD|=2t,|AB|=3t,运用双曲线的定义,可得|AC|,|DC|,再分别在直角三角形ACD和直角三角形ACB中,运用勾股定理,结合双曲线的离心率公式,计算即可得到所求值.
解答  解:如图,设|BD|=t,则|AD|=2t,|AB|=3t,
解:如图,设|BD|=t,则|AD|=2t,|AB|=3t,
由双曲线的定义可得|AC|=|AB|-2a=3t-2a,
由双曲线的定义可得|DC|=|DB|+2a=2a+t,
在直角三角形ACD中,
|AC|2+|AD|2=|CD|2,
即为(3t-2a)2+4t2=(2a+t)2,
化简可得3t=4a,
在直角三角形ACB中,
|AC|2+|AB|2=|CB|2,
即为(3t-2a)2+9t2=(2c)2,
即有4a2+16a2=4c2,即为c2=5a2,
则e=$\frac{c}{a}$=$\sqrt{5}$.
故选:D.
点评 本题考查双曲线的离心率的求法,注意运用定义法和方程思想,以及直角三角形的勾股定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
6.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,其焦距为2c,点Q(c,$\frac{a}{2}$)在椭圆的内部,点P是椭圆C上的动点,且|PF1|+|PQ|<5|F1F2|恒成立,则椭圆离心率的取值范围是( )
| A. | ($\frac{1}{5}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{3}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{2}{5}$,$\frac{\sqrt{2}}{2}$) |
12.今有苹果m个(m∈N+),分给10个同学,每个同学都分到苹果,恰好全部分完.第一个人分得全部苹果的一半还多一个,第二个人分得第一个人余下苹果的一半还多一个,以此类推,后一个人分得前一个人余下的苹果的一半还多一个,则苹果个数m为( )
| A. | 2046 | B. | 1024 | C. | 2017 | D. | 2018 |
2.如图是由圆柱与两个半球组合而成的几何体的三视图,则该几何体的体积与表面积分别为( )
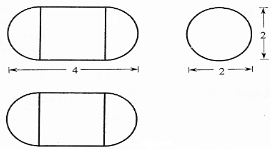

| A. | $\frac{10}{3}π,8π$ | B. | $\frac{16}{3}π,8π$ | C. | $\frac{10}{3}π,10π$ | D. | $\frac{16}{3}π,10π$ |
9.已知集合M={x|x2≤9},N={x|x≤1},则M∩N=( )
| A. | [-3,1] | B. | [1,3] | C. | [-3,3] | D. | (-∞,1] |
6.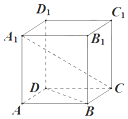 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
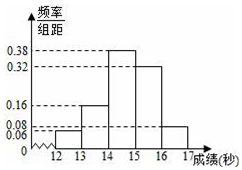 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.