题目内容
14.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$-2$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2,则$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{8}$.分析 运用两边平方,结合向量的数量积的性质:向量的平方即为模的平方,化简整理即可得到所求值.
解答 解:|$\overrightarrow{a}$-2$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2,
两边平方可得,|$\overrightarrow{a}$-2$\overrightarrow{b}$|2=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|2=4,
即有$\overrightarrow{a}$2-4$\overrightarrow{a}$•$\overrightarrow{b}$+4$\overrightarrow{b}$2=1,$\overrightarrow{a}$2+4$\overrightarrow{a}$•$\overrightarrow{b}$+4$\overrightarrow{b}$2=4,
两式相减可得,8$\overrightarrow{a}$•$\overrightarrow{b}$=3,
即为$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{3}{8}$,
故答案为:$\frac{3}{8}$.
点评 本题考查向量的数量积的性质:向量的平方即为模的平方,注意运用平方思想,属于基础题.

练习册系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的外接球的表面积是( )
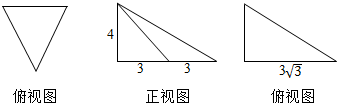

| A. | 208π | B. | 128π | C. | 64π | D. | 32π |
3.若实数x,y满足$\left\{\begin{array}{l}{x-2y≤0}\\{2x-y≥0}\\{x+y≥3}\end{array}\right.$,则下列不等成立的是( )
| A. | x2+y2≥5 | B. | $\frac{y}{x-2}$≥-2 | C. | 2x+y≥5 | D. | |x+3y-1|≥4 |