题目内容
11.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=3x+1-3,则f(-1)的值为( )| A. | -6 | B. | -3 | C. | -2 | D. | 6 |
分析 根据函数奇偶性的性质,将f(-1)转化为f(1)进行求解即可.
解答 解:∵f(x)为定义在R上的奇函数,
∴f(-1)=-f(1),
∵当x≥0时,f(x)=3x+1-3,
∴f(1)=6,
即f(-1)=-f(1)=-6.
故选A.
点评 本题主要考查函数奇偶性的应用,利用函数奇偶性的性质将f(-1)转化为f(1)是解决本题的关键.

练习册系列答案
相关题目
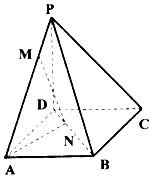 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.