题目内容
13.不同直线m,n和不同平面α,β,给出下列命题,其中真命题有( )①$\left.{\begin{array}{l}{α∥β}\\{m?α}\end{array}}\right\}⇒m∥β$;②$\left.{\begin{array}{l}{m∥n}\\{m∥β}\end{array}}\right\}⇒n∥β$;③$\left.{\begin{array}{l}{n?β}\\{m?α}\end{array}}\right\}⇒m,n异面$;④$\left.{\begin{array}{l}{α⊥β}\\{m∥α}\end{array}}\right\}⇒m⊥β$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 由面面平行的性质定理得①正确;在②中,n∥β或n?β;在③中,m,n相交、平行或异面;在④中,m与β相交、平行或m?β.
解答 解:由不同直线m,n和不同平面α,β,知:
①$\left.{\begin{array}{l}{α∥β}\\{m?α}\end{array}}\right\}⇒m∥β$,由面面平行的性质定理得①正确;
②$\left.{\begin{array}{l}{m∥n}\\{m∥β}\end{array}}\right\}⇒n∥β$或n?β,故②错误;
③$\left.{\begin{array}{l}{n?β}\\{m?α}\end{array}}\right\}⇒m,n异面$、相交或平行,故③错误;
④$\left.{\begin{array}{l}{α⊥β}\\{m∥α}\end{array}}\right\}⇒$m与β相交、平行或m?β,故④错误.
故选:B.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.函数$f(x)=\left\{\begin{array}{l}2{x^3}+3{x^2}+1(x≤0)\\{e^{ax}}(x>0)\end{array}\right.$在[-2,3]上的最大值为2,则实数a的取值范围是( )
| A. | $[\frac{1}{3}ln2,+∞)$ | B. | $[0,\frac{1}{3}ln2]$ | C. | (-∞,0] | D. | $(-∞,\frac{1}{3}ln2]$ |
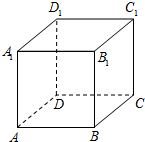 如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)
如图,已知正方体ABCD-A1B1C1D,若在其12条棱中随机地取3条,则这三条棱两两是异面直线的概率是$\frac{2}{55}$(结果用最简分数表示)