题目内容
9.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=30°,b=2,如果这样的三角形有且只有一个,则a的取值范围为a=1或a≥2.分析 由题意求出bsinA=1,数形结合可得a的范围.
解答  解:∵在△ABC中A=30°,b=2,∴bsinA=2×$\frac{1}{2}$=1,
解:∵在△ABC中A=30°,b=2,∴bsinA=2×$\frac{1}{2}$=1,
∵这样的三角形有且只有一个,∴a=1或a≥2,
故答案为:a=1或a≥2.
点评 本题考查正弦定理解决三角形解得个数问题,数形结合是解决问题的关键,属基础题.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 两两相交的三条直线共面 | |
| B. | 两条异面直线在同一平面上的射影可以是一条直线 | |
| C. | 一条直线上有两点到平面的距离相等,则这条直线和该平面平行 | |
| D. | 不共面的四点中,任何三点不共线. |
17.已知$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,则“|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
14.方程C${\;}_{16}^{{x}^{2}-x}$=C${\;}_{16}^{5x-5}$的解集是( )
| A. | {1,3,5,7} | B. | {1,3,5} | C. | {3,5} | D. | {1,3} |
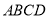 中,
中, ,平面
,平面 平面
平面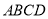 ,四边形
,四边形 是矩形,
是矩形, ,点
,点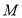 在线段
在线段 .
. 
 平面
平面 为何值时,
为何值时, 平面
平面 ?证明你的结论.
?证明你的结论.