题目内容
4.(1+2x)(x+$\frac{2}{x}$)5展开式中x的系数为40.分析 展开式的x项来源于第一个括号的1和m=(x+$\frac{2}{x}$)5展开式的x项的乘积或第一个括号的2x和m=(x+$\frac{2}{x}$)5展开式的常数项的乘积,分别由m的展开式可得.
解答 解:展开式的x项来源于第一个括号的1和m=(x+$\frac{2}{x}$)5展开式的x项的乘积
或第一个括号的2x和m=(x+$\frac{2}{x}$)5展开式的常数项的乘积,
又m=(x+$\frac{2}{x}$)5的通项为Tk+1=${C}_{5}^{k}$x5-k($\frac{2}{x}$)k=2k•${C}_{5}^{k}$x5-2k,
令5-2k=1可得k=2,故m展开式中含x的项为40x,
令5-2k=0可得k=$\frac{5}{2}$∉Z,故m展开式中无常数项,
∴原式展开式中x的系数为40,
故答案为:40.
点评 本题考查二项式定理和二项式系数,分类讨论是解决问题的关键,属基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.将函数y=(x+1)2的图象按向量$\overrightarrow{a}$经过一次平移后,得到y=x2的图象,则向量$\overrightarrow{a}$=( )
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
12.下列各数中,最大的一个数是( )
| A. | 110(2) | B. | 18 | C. | 14(8) | D. | 20(5) |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|-|PF2|=4b,则双曲线的离心率为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
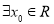 使不等式
使不等式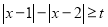 成立.
成立. 的集合
的集合 ;
;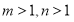 ,对
,对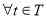 ,不等式
,不等式 恒成立,求
恒成立,求 的最小值.
的最小值.