题目内容
2.首项为1,且公比为q(|q|≠1)的等比数列的第11项等于这个数列的前n项之积,则n的值为( )| A. | 5 | B. | 4 | C. | 6 | D. | 7 |
分析 由an=1•qn-1=qn-1知a11=q10,a1•a2•a3•…•an=${q}^{\frac{n(n-1)}{2}}$,从而求得.
解答 解:由题意知,an=1•qn-1=qn-1,
∴a11=q10,
a1•a2•a3•…•an=q•q2•…•qn-1=${q}^{\frac{n(n-1)}{2}}$,
∴10=$\frac{n(n-1)}{2}$,
∴n=5;
故选:A.
点评 本题考查了等比数列的性质的判断与应用,同时考查了转化思想的应用.

练习册系列答案
相关题目
14.由曲线y=$\sqrt{x}$,直线y=x所围成的封闭曲线的面积是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 1 |
14.F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点.过点F向C的-条渐近线引垂线,垂足为A,交另一条渐近线于点B,若3$\overrightarrow{AF}$=$\overrightarrow{FB}$,则C的心离心率是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{14}}{3}$ |
11.若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,($\overrightarrow{a}$+$\overrightarrow{b}$)$•\overrightarrow{b}$=6,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
18.将函数y=(x+1)2的图象按向量$\overrightarrow{a}$经过一次平移后,得到y=x2的图象,则向量$\overrightarrow{a}$=( )
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
9.将函数y=sinx的图象向右平移$\frac{π}{6}$个单位,再将所得函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+φ),(ω>0,|φ|<$\frac{π}{2}$)的图象,则( )
| A. | ω=2,φ=-$\frac{π}{6}$ | B. | ω=2,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ |
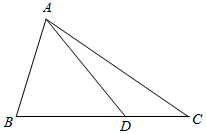 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.