题目内容
20.下列说法正确的是( )| A. | 两两相交的三条直线共面 | |
| B. | 两条异面直线在同一平面上的射影可以是一条直线 | |
| C. | 一条直线上有两点到平面的距离相等,则这条直线和该平面平行 | |
| D. | 不共面的四点中,任何三点不共线. |
分析 利用平面的基本性质、线面位置关系,即可得出结论.
解答 解:两两相交的三条直线,交于同一点时,不共面,故A不正确;
两条异面直线在同一平面上的射影可以是两条相交直线、两条平行直线、一条直线和不在这条直线上的一个点等,不可以是一条直线,故B不正确;
一条直线上有两点到平面的距离相等,则这条直线和该平面平行或相交,故C不正确;
假设任意三点共线,则四个点必共面,与不共面的四点矛盾,故D正确.
故选:D.
点评 本题主要考查了平面的基本性质、线面位置关系,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
14.F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点.过点F向C的-条渐近线引垂线,垂足为A,交另一条渐近线于点B,若3$\overrightarrow{AF}$=$\overrightarrow{FB}$,则C的心离心率是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{14}}{3}$ |
9.将函数y=sinx的图象向右平移$\frac{π}{6}$个单位,再将所得函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+φ),(ω>0,|φ|<$\frac{π}{2}$)的图象,则( )
| A. | ω=2,φ=-$\frac{π}{6}$ | B. | ω=2,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ |
12.下列各数中,最大的一个数是( )
| A. | 110(2) | B. | 18 | C. | 14(8) | D. | 20(5) |
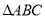 顶点坐标分别是
顶点坐标分别是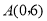 ,
,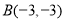 ,
,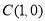 ,将
,将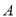 的对应点
的对应点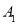 的坐标是
的坐标是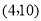 ,则点
,则点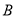 的对应点
的对应点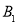 的坐标为( )
的坐标为( )