题目内容
18.若复数z满足z(1-i)=|1-i|+i,则z的实部为$\frac{\sqrt{2}-1}{2}$.分析 设z=a+bi,利用复数代数形式的混合运算法则及模的性质能求出z的实部.
解答 解:设z=a+bi,
∵z(1-i)=|1-i|+i,
∴$(a+bi)(1-i)=\sqrt{1+1}+i$,
∴(a+b)+(b-a)i=$\sqrt{2}+i$,
∴$\left\{\begin{array}{l}{a+b=\sqrt{2}}\\{b-a=1}\end{array}\right.$,
解得a=$\frac{\sqrt{2}-1}{2}$,b=$\frac{\sqrt{2}+1}{2}$,
∴z的实部a=$\frac{\sqrt{2}-1}{2}$.
故答案为:$\frac{\sqrt{2}-1}{2}$.
点评 本题考查复数的实部的求法,是基础题,解题时要认真审题,注意复数代数形式的混合运算法则及模的性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.将函数y=sinx的图象向右平移$\frac{π}{6}$个单位,再将所得函数图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y=sin(ωx+φ),(ω>0,|φ|<$\frac{π}{2}$)的图象,则( )
| A. | ω=2,φ=-$\frac{π}{6}$ | B. | ω=2,φ=-$\frac{π}{3}$ | C. | ω=$\frac{1}{2}$,φ=-$\frac{π}{6}$ | D. | ω=$\frac{1}{2}$,φ=-$\frac{π}{3}$ |
13.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|-|PF2|=4b,则双曲线的离心率为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
 有两个不相等的实数根,则
有两个不相等的实数根,则 的值可以是 (写出一个即可).
的值可以是 (写出一个即可).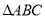 顶点坐标分别是
顶点坐标分别是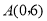 ,
,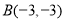 ,
,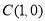 ,将
,将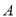 的对应点
的对应点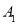 的坐标是
的坐标是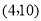 ,则点
,则点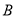 的对应点
的对应点 的坐标为( )
的坐标为( )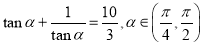 ,则
,则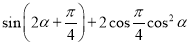 的值为___________.
的值为___________.