题目内容
1.已知正方体ABCD-A1B1C1D1中,体对角线AC1与正方体的内切球面相交于E,F,且E点靠近A点,若正方体的边长为1,则DE与CF所成角的余弦值为$\frac{1+2\sqrt{3}}{11}$.分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出DE与CF所成角的余弦值.
解答 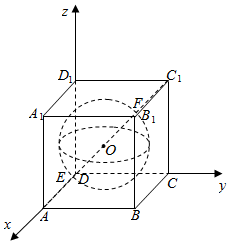 解以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
OE=OF=$\frac{1}{2}$,OA=OC1=$\frac{\sqrt{3}}{2}$,
O($\frac{1}{2},\frac{1}{2},\frac{1}{2}$),A(1,0,0),C1(0,1,1),D(0,0,0),
$\overrightarrow{AO}$=(-$\frac{1}{2},\frac{1}{2},\frac{1}{2}$),$\overrightarrow{O{C}_{1}}$=(-$\frac{1}{2},\frac{1}{2},\frac{1}{2}$),
$\overrightarrow{OE}=\frac{1}{\sqrt{3}}\overrightarrow{OA}$=($\frac{1}{2\sqrt{3}}$,-$\frac{1}{2\sqrt{3}}$,-$\frac{1}{2\sqrt{3}}$),E($\frac{1}{2}+$$\frac{1}{2\sqrt{3}}$,$\frac{1}{2}-$$\frac{1}{2\sqrt{3}}$,$\frac{1}{2}-$$\frac{1}{2\sqrt{3}}$),
$\overrightarrow{OF}=\frac{1}{\sqrt{3}}\overrightarrow{O{C}_{1}}$=(-$\frac{1}{2\sqrt{3}}$,$\frac{1}{2\sqrt{3}}$,$\frac{1}{2\sqrt{3}}$),F($\frac{1}{2}-\frac{1}{2\sqrt{3}}$,$\frac{1}{2}+\frac{1}{2\sqrt{3}}$,$\frac{1}{2}+\frac{1}{2\sqrt{3}}$),
$\overrightarrow{DE}$=($\frac{1}{2}+$$\frac{1}{2\sqrt{3}}$,$\frac{1}{2}-$$\frac{1}{2\sqrt{3}}$,$\frac{1}{2}-$$\frac{1}{2\sqrt{3}}$),$\overrightarrow{CF}$=($\frac{1}{2}-\frac{1}{2\sqrt{3}}$,$\frac{1}{2\sqrt{3}}-\frac{1}{2}$,$\frac{1}{2}+\frac{1}{2\sqrt{3}}$),
设DE与CF所成角为θ,
cosθ=$\frac{|\overrightarrow{DE}•\overrightarrow{CF}|}{|\overrightarrow{DE}|•|\overrightarrow{CF}|}$=$\frac{\frac{1}{2\sqrt{3}}}{\sqrt{1-\frac{1}{2\sqrt{3}}}•\sqrt{1-\frac{1}{2\sqrt{3}}}}$=$\frac{1+2\sqrt{3}}{11}$.
∴DE与CF所成角的余弦值为$\frac{1+2\sqrt{3}}{11}$.
点评 本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| A. | 110(2) | B. | 18 | C. | 14(8) | D. | 20(5) |
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
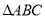 顶点坐标分别是
顶点坐标分别是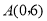 ,
,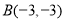 ,
,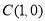 ,将
,将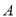 的对应点
的对应点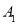 的坐标是
的坐标是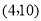 ,则点
,则点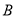 的对应点
的对应点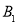 的坐标为( )
的坐标为( )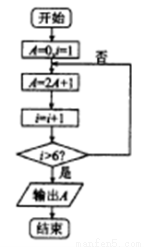
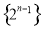 前5项的和 B.计算数列
前5项的和 B.计算数列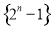 前5项的和
前5项的和