题目内容
已知f(x)在R上是奇函数,且f(x+4)=f(x),f(1)=2,f(2015)= .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:分别应用奇函数的定义和周期函数的定义,将f(2015)变形到-f(1),再由f(1)=2,即可得到答案.
解答:
解:∵f(x)在R上是奇函数,∴f(-x)=-f(x),
∵f(x)=f(x+4),
∴函数f(x)的最小正周期为4,
∴f(2015)=f(4×503+3)=f(3)
=f(3-4)=f(-1)=-f(1),
∵f(1)=2,∴f(2015)=-2,
故答案为:-2.
∵f(x)=f(x+4),
∴函数f(x)的最小正周期为4,
∴f(2015)=f(4×503+3)=f(3)
=f(3-4)=f(-1)=-f(1),
∵f(1)=2,∴f(2015)=-2,
故答案为:-2.
点评:本题主要考查函数的奇偶性和周期性的定义及应用,是一道基础题.

练习册系列答案
相关题目
已知角θ的顶点与原点重合,始边与x轴的正半轴重合,角θ的正弦线长为
,则cos2θ=( )
| ||
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,若
a=2bsinA,则B为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设等差数列{an}的前n项和为Sn,且满足S15>0,S16<0,则当Sn最大时,n=( )
| A、6 | B、7 | C、8 | D、9 |

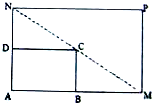 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过C点,已知AB=3米,AD=2米.