题目内容
13．已知双曲线${x^2}-\frac{y^2}{m}=1$（m＞0）渐近线方程为y=±$\sqrt{3}$x，则m的值为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 求出双曲线${x^2}-\frac{y^2}{m}=1$（m＞0）的渐近线方程为y=±$\sqrt{m}$x，可得m的方程，解方程可得m的值．
解答 解：双曲线${x^2}-\frac{y^2}{m}=1$（m＞0）的渐近线方程为y=±$\sqrt{m}$x，
由渐近线方程为y=±$\sqrt{3}$x，可得$\sqrt{m}$=$\sqrt{3}$，
可得m=3，
故选：C．
点评 本题考查双曲线的方程和性质，主要是渐近线方程的运用，考查运算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
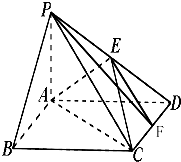如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AD=1，AB=$\sqrt{3}$，点E为PD的中点，点F在棱DC上移动．
如图，在边长为4的菱形ABCD中，∠BAD=60°，DE⊥AB于点E，将△ADE沿DE折起到△A1DE的位置，使A1E⊥EB．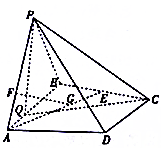
如图，在四棱锥P-ABCD中，侧面PAB⊥底面ABCD，△PAB为正三角形，AB⊥AD，CD⊥AD，点E为线段BC的中点，F，G分别为线段PA，AE上一点，且AB=AD=2，PF=2FA．
8．四面体ABCD中∠BAC=∠BAD=∠CAD=60°，AB=2，AC=3，AD=4，则四面体ABCD的体积V=（ ）
| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 4 | D． | 4$\sqrt{3}$ |
18．若点P（a，b）是直线$y=\sqrt{3}x-\sqrt{3}$上的点，则（a+1）2+b2的最小值是（ ）
| A． | 3 | B． | $\sqrt{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | 0 |
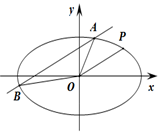如图：已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$，与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点，且椭圆C过点P（2，1），若直线l与直线OP平行且与椭圆C相交于点A，B．
2．设集合M={x|x≥2}，N={x|x2-25＜0}，则M∩N=（ ）
| A． | （1，5） | B． | [2，5） | C． | （-5，2] | D． | [2，+∞） |