��Ŀ����
9����֪��P��2��$\sqrt{2}$������Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ϵ�һ�㣬����Բ��������Ϊ$\frac{\sqrt{2}}{2}$������A��-����0����������ֱ��l1��l2�ֱ���Բ��E��F���㣬��y����M��N���㣬E��M�����㲻�غϣ���E��F����ԭ��Գƣ���1������Բ�ķ��̣�
��2����MNΪֱ����Բ�Ƿ�x���ڶ���Q�����ǣ������Q�����ꣻ������˵�����ɣ�
���� ��1����e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��a=$\sqrt{2}$c����a2=2b2����P��2��$\sqrt{2}$��������Բ���̼������a��b��ֵ�������Բ�ķ��̣�
��2����ֱ��EF����y=kx��k��0����������Բ���̣���õ�E���꣬���ֱ��AE���̷��̣���x=0�����M�����꣬ͬ�����N�����꣬��$\overrightarrow{MQ}$•$\overrightarrow{NQ}$=0���������tֵ�������Q�����ꣻ
��� �⣺��1����Բ��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$��a=$\sqrt{2}$c����a2=2b2��
��P��2��$\sqrt{2}$������$\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$�����a2=8��b2=4��
����Բ�ķ���$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$��
��2����Բ���㣨-2$\sqrt{2}$��0������E��F����ԭ��Գƣ�
��ֱ��EF����y=kx��k��0����
$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$����E��$\frac{2\sqrt{2}}{\sqrt{1+2{k}^{2}}}$��$\frac{2\sqrt{2}k}{\sqrt{1+2{k}^{2}}}$����
��ֱ��AE����y=$\frac{k}{1+\sqrt{1+2{k}^{2}}}$��x+2$\sqrt{2}$����
��x=0��y=$\frac{2\sqrt{2}k}{1+\sqrt{1+2{k}^{2}}}$��
���M��0��$\frac{2\sqrt{2}k}{1+\sqrt{1+2{k}^{2}}}$����ͬ����֪N��0��$\frac{2\sqrt{2}k}{1-\sqrt{1+2{k}^{2}}}$����
������x���ϴ��ڶ���Q��t��0�������MQNΪֱ�ǣ�
��$\overrightarrow{MQ}$•$\overrightarrow{NQ}$=0��
��t2+$\frac{-2\sqrt{2}k}{1+\sqrt{1+2{k}^{2}}}$��$\frac{-2\sqrt{2}k}{1-\sqrt{1+2{k}^{2}}}$=0��t2-4=0��
��ã�t=2��t=-2��
�ʴ��ڵ�Q��2��0����Q��-2��0����MNΪֱ����Բ��x���ڴ˶��㣮
���� ���⿼����Բ�ı����̼��������ʣ�ֱ������Բ��λ�ù�ϵ�������������������������㣬������������������е��⣮

 �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�| A�� | [8��10] | B�� | ��6��+�ޣ� | C�� | ��6��8] | D�� | [8��+�ޣ� |
| A�� | 3 | B�� | $\sqrt{3}$ | C�� | $\frac{{\sqrt{3}}}{2}$ | D�� | 0 |
| �¶�t���棩 | -5 | 0 | 6 | 8 | 12 | 15 | 20 |
| �����ٶ�y | 2 | 4 | 5 | 6 | 7 | 8 | 10 |
��2�����ã�1���е����Իع鷽�̣��������´�-50C��200Cʱ�����ٶȵı仯��������ij�µ�ƽ��������20Cʱ��Ԥ�����´�Լ���������٣�
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��$\hat b=\frac{{\sum_{i=1}^n{��{{x_i}-\overline x}����{{y_i}-\overline y}��}}}{{\sum_{i=1}^n{{{��{{x_i}-\overline x}��}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline{xy}}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}��\hat a=\overline y-\hat b\overline x$��
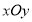 �У���ԭ��
�У���ԭ��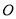 Ϊ���㣬��
Ϊ���㣬�� ���������Ϊ���Ὠ��������ϵ����֪����
���������Ϊ���Ὠ��������ϵ����֪����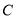 �ļ����귽��Ϊ
�ļ����귽��Ϊ ��
��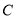 ��ֱ�����귽�̲�ָ������״��
��ֱ�����귽�̲�ָ������״��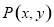 ������
������ �ϵĶ��㣬��
�ϵĶ��㣬�� ��ȡֵ��Χ��
��ȡֵ��Χ��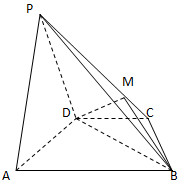 ��ͼ��������P-ABCD�У�AD=4��BD=8��ƽ��PAD��ƽ��ABCD��AB=2DC=4$\sqrt{5}$��
��ͼ��������P-ABCD�У�AD=4��BD=8��ƽ��PAD��ƽ��ABCD��AB=2DC=4$\sqrt{5}$��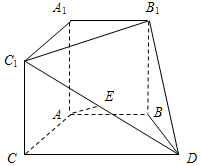 ����ͼ��ʾ�ļ������У�A1B1C1-ABC��ֱ���������ı���ABDC�����Σ�AB��CD����$AB=BD=\frac{1}{2}CD=2$����BDC=60�㣬E��C1D���е㣮
����ͼ��ʾ�ļ������У�A1B1C1-ABC��ֱ���������ı���ABDC�����Σ�AB��CD����$AB=BD=\frac{1}{2}CD=2$����BDC=60�㣬E��C1D���е㣮 ��ͼ���ڱ߳�Ϊ4������ABCD�У���BAD=60�㣬DE��AB�ڵ�E������ADE��DE����A1DE��λ�ã�ʹA1E��EB��
��ͼ���ڱ߳�Ϊ4������ABCD�У���BAD=60�㣬DE��AB�ڵ�E������ADE��DE����A1DE��λ�ã�ʹA1E��EB��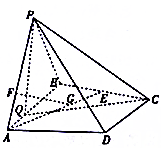 ��ͼ��������P-ABCD�У�����PAB�͵���ABCD����PABΪ�������Σ�AB��AD��CD��AD����EΪ�߶�BC���е㣬F��G�ֱ�Ϊ�߶�PA��AE��һ�㣬��AB=AD=2��PF=2FA��
��ͼ��������P-ABCD�У�����PAB�͵���ABCD����PABΪ�������Σ�AB��AD��CD��AD����EΪ�߶�BC���е㣬F��G�ֱ�Ϊ�߶�PA��AE��һ�㣬��AB=AD=2��PF=2FA��