题目内容
8.如果b是a,c的等差中项,y是x,z的等比中项,且x,y,z都是正数,则(b-c)logmx+(c-a)logmy+(a-b)logmz=0.分析 由等差数列,可设公差为d,则a=b-d,c=b+d,y是x,z的等比中项,可得xz=y2,运用对数的运算性质,计算即可得到所求值.
解答 解:b是a,c的等差中项,
可设公差为d,则a=b-d,c=b+d,
y是x,z的等比中项,可得xz=y2,
则(b-c)logmx+(c-a)logmy+(a-b)logmz
=-dlogmx+2dlogmy+(-d)logmz
=-d(logmx+logmz)+dlogmy2=-dlogmxz+dlogmy2
=-dlogm$\frac{xz}{{y}^{2}}$=-dlogm1=0.
故答案为:0.
点评 本题考查等差数列和等比数列中项的性质,考查对数的运算性质,化简整理的运算能力,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
10. 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )| A. | 6 | B. | 25 | C. | 100 | D. | 400 |
18.若点P(a,b)是直线$y=\sqrt{3}x-\sqrt{3}$上的点,则(a+1)2+b2的最小值是( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 0 |
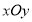 中,以原点
中,以原点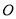 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线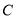 的极坐标方程为
的极坐标方程为 .
.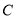 的直角坐标方程并指出其形状;
的直角坐标方程并指出其形状;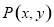 是曲线
是曲线 上的动点,求
上的动点,求 的取值范围.
的取值范围. ,若
,若 ,则实数
,则实数 等于( )
等于( ) B.
B. C.2 D.4
C.2 D.4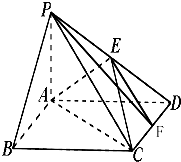 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.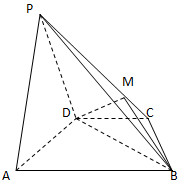 如图,在四棱锥P-ABCD中,AD=4,BD=8,平面PAD⊥平面ABCD,AB=2DC=4$\sqrt{5}$.
如图,在四棱锥P-ABCD中,AD=4,BD=8,平面PAD⊥平面ABCD,AB=2DC=4$\sqrt{5}$.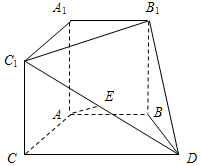 在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.
在如图所示的几何体中,A1B1C1-ABC是直三棱柱,四边形ABDC是梯形,AB∥CD,且$AB=BD=\frac{1}{2}CD=2$,∠BDC=60°,E是C1D的中点.