题目内容

在直角三角形ABC中，∠A=90°，BC=a，若长为2a的线段PQ以点A为中点，问
PQ
与
BC
的夹角θ取何值时，
BP
•
CQ
的值最大？并求出这个最大值．
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：以直角顶点A为坐标原点，两直角边所在的直线为坐标轴，建立平面直角坐标系，设点P的坐标为（x，y），
则建立
BP
•
CQ
与
PQ
与
BC
的夹角θ的函数关系式进行求解．
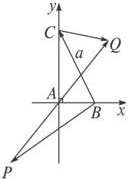解答： 解：如图
以直角顶点A为坐标原点，两直角边所在的直线为坐标轴，建立如图所示的平面直角坐标系．设|AB|=c，|AC|=b，则A（0，0），B（c，0），C（0，b），且|PQ|=2a，|BC|=a．
设点P的坐标为（x，y），
则Q（-x，-y）．
∴
BP
=（x-c，y），
CQ
=（-x，-y-b），
BC
=（-c，b），
PQ
=（-2x，-2y）．
∴
BP
•
CQ
=（x-c）（-x）+y（-y-b）=-（x2+y2）+cx-by．
∵cosθ=
BP
•
CQ
|
BP
||
CQ
|
=
cx-by
a2
，
∴cx-by=a2cosθ．
∴
BP
•
CQ
=-a2+a2cosθ．
故当cosθ=1，即θ=0，
PQ
与
BC
的方向相同时，
BP
•
CQ
最大，其最大值为0．
点评：本题考查向量数量积的计算，函数思想．
练习册系列答案
相关题目
已知函数f（x）=
1，x＞1
1-x2
，-1≤x≤1
|x|，x＜-1
，求f（3）+f（-3）f（
1
3
）的值．
已知函数f（x）=
-x-1，(x＜-2)
x+3，(-2≤x≤
1
2
)
5x+1，(x＞
1
2
)
（x∈R），求函数f（x）的最小值．
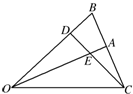如图所示，已知△AOB中，点C与点B关于点A对称，
OD
=2
DB
，DC和OA交于点E，设O
A
=
a
，
OB
=
b
．
（1）用
a
和
b
表示向量
OC
，
DC
；
（2）若
OE
=
λOA
，求实数λ的值．
已知|
a
|=2，|
b
|=3，
a
与
b
的夹角为θ，且tan（
π
4
+θ）=-2-
3
，求
a
•
b
与|
a
-
b
|的值．
在正方体ABCD-A1B1C1D1中，与AA1平行的棱有
 
条．
已知二次函数y=f（x）=x2+bx+c的图象过点（1，13），且函数y=f(x-
1
2
)是偶函数．
（1）求f（x）的解析式；
（2）函数y=f（x）的图象上是否存在这样的点，其横坐标是正整数，纵坐标是一个完全平方数？如果存在，求出这样的点的坐标；如果不存在，请说明理由．
已知函数f（x）=x-alnx，g（x）=
lnx
x
．
（Ⅰ） 若函数f（x）存在不大于0的最小值，求实数a的取值范围；
（Ⅱ）设x=1是函数f（x）的极小值点．
（i）若函数f（x）与函数g（x）的图象分别在直线y=kx的两侧，求k的取值范围；
（ii） 若M（x1，y1），N（x2，y2）（0＜x1＜x2）是f（x）图象上的两点，且存在实x0∈（0，+∞）
使得f′（x0）=
f(x2)-f(x1)
x2-x1
，证明：x1＜x0＜x2．
设m、n是两条不同的直线，α，β，γ是三个不同的平面，给出下列四个命题：
①若m⊥α，n∥α，则m⊥n； 
②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m⊥α，n⊥α，则m∥n； 
④若α⊥γ，β⊥γ，则α∥β．
其中正确命题的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网