题目内容
已知等比数列{an},且a4+a6=π,则a5a3+2
+a5a7的值为( )
| a | 2 5 |
| A、2π |
| B、4π2 |
| C、π |
| D、π2 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:由等比数列通项公式把a5a3+2
+a5a7等价转化为a42+2a4a6+a62,再由完全平方和公式得到(a4+a6)2,利用a4+a6=π,能够求出结果.
| a | 2 5 |
解答:
解:∵a4+a6=π,
∴a5a3+2
+a5a7=a42+2a4a6+a62=(a4+a6)2=π2.
故选:D.
∴a5a3+2
| a | 2 5 |
故选:D.
点评:本题考查等比数列的性质和应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
在平面直角坐标系xOy中,角α的终边与单位圆交于点A,点A在第二象限,且点A的横坐标与纵坐标之比为-
,则
的值为( )
| 1 |
| 2 |
| cos2α-sin2α |
| sin2α+2cos2α |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
设a=20.5,b=0.32,c=log20.3,则a、b、c的大小关系是( )
| A、a<b<c |
| B、b<a<c |
| C、c<b<a |
| D、b<c<a |
在△ABC中,角A,B,C的对边分别为a,b,c,若(a2+c2-b2)tanB=
ac,则角B的值为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行如图的程序框图,若M=
,则输出的n=( )

| 7 |
| 8 |

| A、2 | B、3 | C、4 | D、5 |


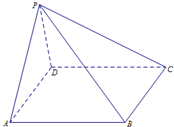 已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,且∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积是( )
已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,且∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积是( )