题目内容
20.已知实数x满足9x-12•3x+27≤0,函数$f(x)={log_2}\frac{x}{2}•{log_{\sqrt{2}}}\frac{{\sqrt{x}}}{2}$.(1)求实数x的取值范围;
(2)求函数f(x)的最大值和最小值,并求出此时x的值.
分析 (1)问题转化为(3x-3)(3x-9)≤0,求出x的范围即可;
(2)将f(x)的解析式配方,结合二次函数的性质求出f(x)的最大值和最小值即可.
解答 解:(1)由9x-12•3x+27≤0,
得(3x)2-12•3x+27≤0,
即(3x-3)(3x-9)≤0,
∴3≤3x≤9,1≤x≤2.
(2)因为$f(x)={log_2}\frac{x}{2}•{log_{\sqrt{2}}}\frac{{\sqrt{x}}}{2}=({log_2}x-1)({log_2}x-2)$
=${({log_2}x)^2}-3{log_2}x+2={({log_2}x-\frac{3}{2})^2}-\frac{1}{4}$,
∵1≤x≤2,∴0≤log2x≤1,
当log2x=1,即x=2时,f(x)min=0,
当log2x=0,即x=1时,f(x)max=2.
点评 本题考查了对数函数以及二次函数的性质,考查函数的单调性问题,是一道中档题.

练习册系列答案
相关题目
11.复数z=$\frac{(i-1)^{2}+2}{i+1}$的实部为( )
| A. | -2 | B. | -1 | C. | 1、 | D. | 0 |
8.口袋中装有一些大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.43,摸出白球的概率是0.27,那么摸出黑球的概率是( )
| A. | 0.43 | B. | 0.27 | C. | 0.3 | D. | 0.7 |
5.若点A的坐标是(3,2),F是抛物线y2=2x的焦点,点P在抛物线上移动,为使得|PA|+|PF|取得最小值,则P点的坐标是( )
| A. | (1,2) | B. | (2,1) | C. | (2,2) | D. | (0,1) |
12.已知圆C方程x2+y2-2x-4y+a=0,圆C与直线x+2y-4=0相交于A,B两点,且OA⊥OB(O为坐标原点),则实数a的值为( )
| A. | $-\frac{4}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{1}{5}$ |
10.书架上有2本不同的语文书,1本数学书,从中任意取出2本,取出的书恰好都是语文书的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
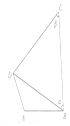 如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).
如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).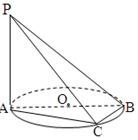 已知AB是圆O的直径,C为底面圆周上一点,PA⊥平面ABC,
已知AB是圆O的直径,C为底面圆周上一点,PA⊥平面ABC,