Question

【题目】以表示值域为的函数组成的集合，表示具有如下性质的函数组成的集合：对于函数，存在一个正数，使得函数的值域包含于区间。例如，当，时，，。则下列命题中正确的是：（ ）

A.设函数的定义域为，则“”的充要条件是“，，”

B.函数的充要条件是有最大值和最小值

C.若函数，的定义域相同，且，，则

D.若函数有最大值，则

Answer 1

【答案】ACD

【解析】

A选项中，根据函数的定义域、值域的定义，转化成用简易逻辑语言表示出来；

B选项中举反例保证函数的值域为集合的子集，但值域是一个开区间，从而说明函数没有最值；C选项中从并集的角度认识函数值域，可以发现，从而发现命题正确；D选项中从极限的角度证明，均不成立，所以，再求出函数的值域为，从而得到命题D正确.

对A，“”即函数值域为，“，，”表示的是函数可以在中任意取值，故有：设函数的定义域为，则“”的充要条件是“，，”，命题A是真命题；

对B，若函数，即存在一个正数，使得函数的值域包含于区间．

．例如：函数满足，则有，此时，无最大值，无最小值．命题B“若函数，则有最大值和最小值．”是假命题；

对C，若函数，的定义域相同，且，，则值域为，，并且存在一个正数，使得，，则．命题C是真命题．

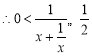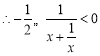对D，函数有最大值，假设，当时，，，，则，与题意不符； 假设，当时，，，，则，与题意不符.，即函数，当时，，，即；当时，；当时，，，即．

，即，故命题D是真命题．

故选：ACD.