题目内容

【题目】已知动点P到定点的距离比它到直线的距离小2，设动点P的轨迹为曲线C．

求曲线C的方程；

若直线与曲线C和圆从左至右的交点依次为A，B，C，D求的值．

【答案】（1）（2）

【解析】

（1）动点到定点的距离比它到直线的距离小2，可转化成：动点P到直线的距离与它到的距离相等，由抛物线的定义及标准方程求解即可。

（2）联立直线与抛物线方程可得两交点的纵坐标：y1＝，y2＝4，利用抛物线的定义把转化成即可求解。

解:（1）由已知动点P到直线的距离与它到的距离相等

的轨迹是以为焦点的抛物线.

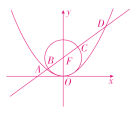
（2）如图所示，抛物线x2＝4y的焦点为F(0,1)，直线3x－4y＋4＝0过点(0,1)，

由，得4y2－17y＋4＝0，

设A，D，则＝， ＝1，

解得＝， ＝4，

则

练习册系列答案
相关题目

【题目】为打赢打好脱贫攻坚战，实现建档立卡贫困人员稳定增收，某地区把特色养殖确定为脱贫特色主导产业，助力乡村振兴.现计划建造一个室内面积为平方米的矩形温室大棚，并在温室大棚内建两个大小、形状完全相同的矩形养殖池，其中沿温室大棚前、后、左、右内墙各保留米宽的通道，两养殖池之间保留2米宽的通道.设温室的一边长度为米，如图所示.

（1）将两个养殖池的总面积表示为的函数，并写出定义域；

（2）当温室的边长取何值时，总面积最大？最大值是多少？

【题目】如图，在三棱柱ABC-中，平面ABC，D，E，F，G分别为，AC，，的中点，AB=BC=，AC==2．

（Ⅰ）求证：AC⊥平面BEF；

（Ⅱ）求二面角B-CD-C1的余弦值；

（Ⅲ）证明：直线FG与平面BCD相交．

【题目】以“你我中国梦，全民建小康”为主题、“社会主义核心价值观”为主线，为了了解两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度，对地区的100名观众进行统计，统计结果如下：

在被调查的全体观众中随机抽取1名“非常满意”的人是地区的概率为0.45，且.

（Ⅰ）现从100名观众中用分层抽样的方法抽取20名进行问卷调查，则应抽取“满意”的地区的人数各是多少？

（Ⅱ）在（Ⅰ）抽取的“满意”的观众中，随机选出3人进行座谈，求至少有两名是地区观众的概率？

（Ⅲ）完成上述表格，并根据表格判断是否有的把握认为观众的满意程度与所在地区有关系？

附： ， .

【题目】已知函数.

（Ⅰ）试判断1是的极大值点还是极小值点，并说明理由；

（Ⅱ）设是函数的导函数，求证： .

【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标，分别从两厂随机各选取了个轮胎，将每个轮胎的宽度（单位： ）记录下来并绘制出如下的折线图：

（1）分别计算甲、乙两厂提供的个轮胎宽度的平均值；

（2）轮胎的宽度在内，则称这个轮胎是标准轮胎.

（i）若从甲乙提供的个轮胎中随机选取个，求所选的轮胎是标准轮胎的概率；

（ii）试比较甲、乙两厂分别提供的个轮胎中所有标准轮胎宽度的方差大小，根据两厂的标准轮胎宽度的平均水平及其波动情况，判断这两个工厂哪个厂的轮胎相对更好？

【题目】已知函数．

(1)若函数的最小值是，且c＝1，，求F(2)＋F(－2)的值；

(2)若a＝1，c＝0，且在区间(0，1]上恒成立，试求b的取值范围.

【题目】若数列满足：对于任意均为数列中的项，则称数列为“ 数列”．

（1）若数列的前项和，求证：数列为“ 数列”；

（2）若公差为的等差数列为“ 数列”，求的取值范围；

（3）若数列为“ 数列”，，且对于任意，均有，求数列的通项公式．

【题目】已知函数的定义域为，且对任意的有. 当时，，.

（1）求并证明的奇偶性；

（2）判断的单调性并证明；

（3）求；若对任意恒成立，求实数的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网