题目内容
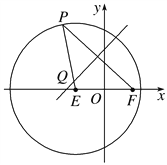
【题目】如图，河的两岸分别有生活小区
和
，其中
，
三点共线，
与
的延长线交于点
，测得
，
，
，
，
，若以
所在直线分别为
轴建立平面直角坐标系
则河岸
可看成是曲线
（其中
是常数）的一部分，河岸
可看成是直线
（其中
为常数）的一部分．
（1）求
的值．
（2）现准备建一座桥
，其中
分别在
上，且
，
的横坐标为
．写出桥的长
关于的函数关系式
，并标明定义域；当为何值时，取到最小值？最小值是多少？
【答案】（1）
，
.（2）
；当
时取到最小值，为
【解析】
（1）计算
，
，
，
，将点代入直线方程计算得到答案.
（2）计算
，得到
，再利用均值不等式计算得到答案.
（1）由题意得：
，
，∴，，，，
把，
代入
得
，解得：，
把，代入
得
，解得.
（2）由（1）得：
点在
上，∴，
①桥
的长
为到直线
的距离，
故
；
②由①得：
，
而
，∴
，
当且仅当
时即“=”成立，∴
.
练习册系列答案
相关题目
