题目内容
已知P是直线l:3x-4y+11=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的两条切线,C是圆心,那么四边形PACB面积的最小值是 ( ).
A.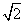 B.2
B.2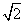 C.
C. D.2
D.2
C解析 圆的标准方程为(x-1)2+(y-1)2=1,圆心为C(1,1),半径为r=1,根据对称性可知,四边形PACB的面积为2S△APC=2×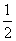 |PA|r=|PA|=
|PA|r=|PA|=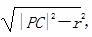 ,要使四边形PACB的面积最小,则只需|PC|最小,最小时为圆心到直线l:3x-4y+11=0的距离d=
,要使四边形PACB的面积最小,则只需|PC|最小,最小时为圆心到直线l:3x-4y+11=0的距离d=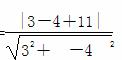 =
=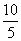 =2.所以四边形PACB面积的最小值为
=2.所以四边形PACB面积的最小值为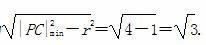
答案 C

练习册系列答案
相关题目
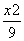 -
-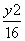 =1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△ PQF的周长为________.
=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△ PQF的周长为________.