题目内容
12.已知函数f(x)的定义域为D,若对于?a,b,c∈D,f(a),f(b),f(c)分别为某个三角形的三边长,则称f(x)为“三角形函数”.给出下列四个函数:①f(x)=lg(x+1)(x>0);
②f(x)=4-cosx;
③$f(x)={x^{\frac{1}{2}}}(1≤x≤16)$;
④$f(x)=\frac{{{3^x}+2}}{{{3^x}+1}}$
其中为“三角形函数”的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设它的三边长分别为a,b,c,则a+b>c,若f(x)为“三角形函数,则满足f(x)max-f(x)min<f(x)min,即可.
解答 解:若f(x)为“三角形函数,
则f(x)max-f(x)min<f(x)min,
①若f(x)=lg(x+1)(x>0),则f(x)∈(0,+∞),不满足条件;
②若f(x)=4-cosx,则f(x)∈[3,5],满足条件;
③若$f(x)={x^{\frac{1}{2}}}(1≤x≤16)$,则f(x)∈[1,4],不满足条件;
④若$f(x)=\frac{{{3^x}+2}}{{{3^x}+1}}$=1+$\frac{1}{{3}^{x}+1}$,则f(x)∈(1,2),满足条件;
故选:B
点评 本题主要考查命题的真假判断,涉及新定义“三角形函数”,根据条件转化为求f(x)max-f(x)min<f(x)min,是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
2.已知函数$f(x)=sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的最小正周期为π,f(x)的图象向左平移$\frac{π}{3}$个单位后关于直线x=0对称,则$f(x+\frac{π}{12})+f(x-\frac{π}{6})$的单调递增区间为( )
| A. | [kπ-$\frac{11π}{24}$,kπ+$\frac{π}{24}$](k∈Z) | B. | $[kπ+\frac{3π}{8},kπ+\frac{7π}{8}](k∈Z)$ | ||
| C. | $[2kπ-\frac{π}{4},2kπ+\frac{3π}{4}](k∈Z)$ | D. | $[2kπ+\frac{3π}{4},2kπ+\frac{7π}{4}](k∈Z)$ |
20.已知$f(x)=\left\{\begin{array}{l}(3-a)x-a,x<1\\{log_a}x,x≥1\end{array}\right.$是(-∞,+∞)上的增函数,那么实数a的取值范围是( )
| A. | (1,+∞) | B. | (1,3) | C. | (0,1)∪(1,3) | D. | $[\frac{3}{2},3)$ |
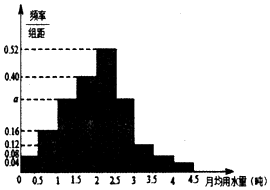 水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.
水是地球上宝贵的资源,由于价格比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.