题目内容
7.已知命题p:函数f(x)=x2-2ax+3在区间[-1,2]单调递增,命题q:函数g(x)=lg(x2+ax+4)定义域为R,若命题“p且q”为假,“p或q”为真,求实数a的取值范围.分析 先求出关于p,q成立的a的范围,根据p,q一真一假,通过讨论得到关于a的不等式组,解出即可
解答 解:命题p为真时:a≤-1;
命题q为真时:a2-16<0即-4<a<4,
因为命题“p∧q”为假,“p∨q”为真,所以$\left\{\begin{array}{l}p真\\ q假\end{array}\right.$或$\left\{\begin{array}{l}p假\\ q真\end{array}\right.$,
即$\left\{\begin{array}{l}a≤-1\\ a≤-4或a≥4\end{array}\right.$,或$\left\{\begin{array}{l}a>-1\\-4<a<4\end{array}\right.$,解得a≤-4或-1<a<4.
所以实数a的取值范围为(-∞,-4]∪(-1,4).
点评 本题考查了复合命题的判断,考查二次函数、对数函数的性质,分类讨论数学,属于中档题.

练习册系列答案
相关题目
18.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$当目标函数z=ax+by(a>0,b>0)在该约束条件下取得最小值1时,则$\frac{1}{3a}+\frac{2}{b}$的最小值为( )
| A. | $4+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3+\sqrt{2}$ |
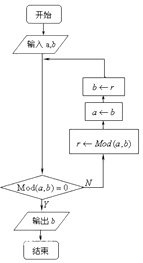 辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.
辗转相除法,又名欧几里得算法,乃求两个正整数之最大公因子的算法.它是已知最古老的算法,在中国则可以追溯至东汉出现的《九章算术》,图中的程序框图所表述的算法就是欧几里得辗转相除法,若输入a=5280,b=12155,则输出的b=55.
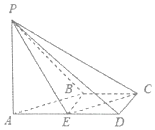 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.